10.4E Uma roda em forma de anel é solta em uma rampa. A força de atrito entre a rampa e a roda é , onde é a força normal que a rampa faz sobre a roda. Calcule o ângulo máximo de inclinação da rampa para que o movimento seja de rolamento.

Belezoca galerinha, como estamos falando de um rolamento no plano inclinado, podemos representar nosso sistema como:

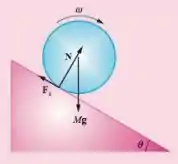
Onde é a força normal, é a nossa força peso e é a nossa força de atrito, dessa maneira, se o corpo rola, quer dizer que ele vai possuir uma aceleração resultante tal que o somatório das forças é:

Mas essa força de atrito é a responsável por gerar o torque que faz o anel rolar, então sendo o raio do anel, teremos que:

E o torque também pode ser expresso como:

Onde é o momento ne inércia do objeto e é aceleração angular do objeto, sendo relacionada com a aceleração linear através da relação , dessa maneira podemos igualar os torques tal que:

De forma que o somatório das forças se torna:

Então se a gente isolar a aceleração, vamos obter:

Onde é o momento de inércia do objeto, nesse caso dado para o anel como , de forma que a aceleração linear será: