Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 9.Exercícios e Problemas - Ex. 19

9.19E Calcule o momento de inércia de um cubo homogêneo de massa M e aresta a em relação a um eixo passando por uma de suas arestas.

Passo 1

Iradoso galera, de acordo com a nossa tabela, os momentos de inércia de um paralelepípedo com lados a ,   b e c , com os eixos passando em cada uma das faces é dada pra gente como:

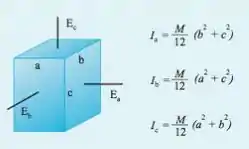
MAAAASS, não temos um paralelepípedo, temos um cubo de lado a , tal que:

a = b = c

Logo o momento de inércia passando por qualquer um dos lados do cubo (afinal são todos iguais) é:

I a = M 12 a 2 + a 2

I a = M 12 2 a 2

I a = M 6 a 2

Passo 2

Beleza, mas esse momento de inércia é pra um eixo que passa pelo centro de uma das faces, só que queremos um eixo que passa em cima de umas das arestas. Então a sagacidade aqui é a gente usar o Teorema dos Eixos Paralelos para deslocar nosso momento de inércia, o teorema nos diz que:

I = I a + M h 2

Onde h   é a distância entre os eixos paralelos, nesse caso temos que a distância do centro de um lado do cubo até uma das extremidades, é igual a metade da diagonal do mesmo lado, de forma que:

h = 1 2 a 2 + a 2

h = 2 2 a

Passo 3

Xuxu no mel, então substituindo nossos valores no teorema, temos que:

I = I a + M h 2

I = M 6 a 2 + M 2 2 a 2

Logo:

I = M 6 a 2 + M 2 a 2

Portanto o momento de inércia em relação a um eixo que passa por uma aresta do cubo de lado a é:

I = 2 3 M a 2

Resposta

I = 2 3 M a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma porta de 15k g e 70c m de largura, suspensa por dobradiças bem azeitadas, esta aberta de 90 ° , ou seja, com seu plano perpendicular ao plano do batente. Ela leva um empurrão na beirada aberta, co
Um pião cônico homogêneo de massa M tem raio da base R e altura h . (a) Calcule a posição do centro de massa do pião. (b) Com o auxilio do resultado do probl. 5, calcule a velocidade angular Ω de prec
Calcule o momento de inércia de uma lamina homogênea de massa M em forma de anel circular de raio interno r 1 e raio externo r 2 , (a) Em relação a um eixo perpendicular ao plano do anel, passadno pel
Como aplicação do teorema dos eixos perpendiculares (Probl. 1), calcule: (a) O momento de inércia para uma placa retangular homohenea de massa M e lados a e b em relação a um eixo perpendicular a seu
O teto da sala de jantar dos estudantes da sua faculdade será apoiado por vigas de madeira cruzadas altas fixadas na forma de um L de cabeça para baixo (Figura 9-73). Cada membro vertical tem 10,0 pés