Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 10.Exercícios e Problemas - Ex. 8

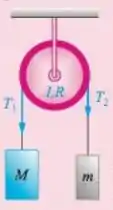
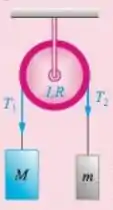
10.8P Na figura 10.12, o cabo rola na roldana sem deslizamento. Calcule a aceleração angular da roldana.

Passo 1

Show de bolinhas galera, nessa situação temos que a roldana está sujeita a duas trações com sentidos contrários, devido a cada força peso que os dois blocos estão submetidos. Vamos chamar essas tensões resultantes de T 1 e T 2 :

De forma que podemos montar um sisteminha de equações, com expressões pra cada bloco, saca só, para o bloco de massa M , temos que:

M g - T 1 = M a

Ou melhor:

T 1 = M g - M a

Agora para o segundo bloco podemos fazer parecido, de forma que:

T 2 - m g = m a

T 2 = m a + m g

Passo 2

Belezoca, já temos as duas trações T 1 e T 2 que geram o torque τ na roldana, de forma que:

τ = τ 1 - τ 2

τ = R T 1 - R T 2

E como o torque também é relacionado através da expressão:

τ = I α

Onde α é a aceleração angular e I é o momento de inércia, tal que:

R T 1 - R T 2 = I α

E então se a gente substituir as trações T 1 e T 2 , num passe de mágica:

R M g - M a - R m a + m g = I α

Passo 3

E agora a sagacidade super hiper master de todos os tempos, é a gente usar a relação entre aceleração angular e linear:

a = α R

Tal que nossa expressão vai se tornar:

R M g - M α R - R m α R + m g = I α

Agora sim, bora isolar a aceleração angular nessa expressão fofíssima ai:

M R g - M α R 2 - m α R 2 - R m g = I α

R g M - m - α R 2 M + m = I α

I α R + α R M + m = g M - m

Logo:

α = g M - m I R + R M + m

α = g R M - m I R 2 + M + m

Resposta

α = g R M - m I R 2 + M + m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma roda de 42,0 cm de diâmetro, que consiste de uma borda e seis raios, é feita de um material plástico rígido, porém fino, com densidade de massa linear de 25,0 g/cm. Essa roda élibertada do repouso
Uma bola de gude homogênea rola para baixo a partir do topo da lateral esquerda de uma tigela simétrica, partindo do repouso. O topo de cada lateral está a uma distância h do fundoda tigela. A metade
Qual fração da energia cinética total é rotacional para os seguintes objetos que rolam sem deslizar sobre uma superfície horizontal? a) Um cilindro maciço e uniforme; b) uma esfera uniforme; c) uma es
Uma bola de boliche rola sem deslizar para cima de uma rampa inclinada de um ângulo β com a horizontal. (Veja o Exemplo 10.7 na Seção 10.3.) Considere a bola uma esfera maciça homogênea e ignore os se
Um fio é enrolado diversas vezes em torno da periferia de um pequeno aro de raio 8,0 cm e massa 0,180 kg. A extremidade livre do fio é mantida fixa e o aro é libertado a partir do repouso (Figura 10.4