Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.3 - Ex. 26
Uma bola de boliche rola sem deslizar para cima de uma rampa inclinada de um ângulo com a horizontal. (Veja o Exemplo 10.7 na Seção 10.3.) Considere a bola uma esfera maciça homogênea e ignore os seus orifícios. a) Faça um diagrama do corpo livre para a bola. Explique por que a força de atrito deve possuir sentido para cima. b) Qual é a aceleração do centro de massa da bola? c) Qual deve ser o coeficiente de atrito estático mínimo para impedir o
deslizamento?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma bola de boliche (maciça e homogênea) rola sem deslizar para cima de uma rampa inclinada de um ângulo com a horizontal.
Queremos fazer um diagrama do corpo livre para a bola e explicar o porquê da força de atrito estar apontada para cima.
Queremos também encontrar a aceleração do centro de massa da bola e o coeficiente de atrito estático mínimo para impedir o deslizamento.
Para isso, vamos aplicar e no movimento da bola de boliche.
Sabemos que:
Onde é o torque, é o momento de inércia, é a aceleração angular, é a força resultante, é a massa, é a aceleração, é o raio, é a força de atrito, é o coeficiente de atrito e é a força normal.
Seja direcionado para baixo da inclinação.
Passo 2
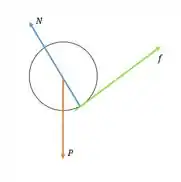
- Esboçando o diagrama de corpo livre dessa situação:
- A força de atrito resulta em uma aceleração angular, dada por
- De qualquer uma das relações acima entre e :
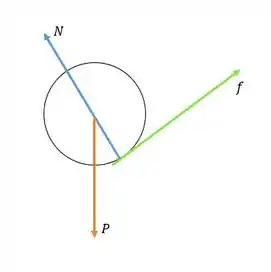
A velocidade angular da bola deve diminuir e, portanto, o torque é proporcionado por uma força de atrito que age subindo a colina.
Passo 3
Aplicando, então, a segunda lei de Newton para p centro de massa:
e a aceleração e aceleração angular estão relacionadas por:
Combinando as equações, ficamos com:
