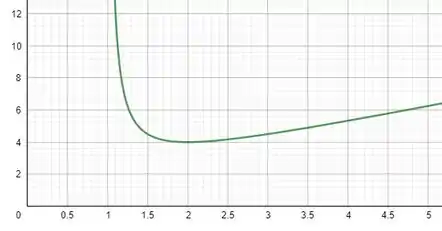
117. Para uma lente com distância focal , determine a menor distância possível entre um objeto e sua imagem real. Faça um gráfico da distância entre o objeto e sua imagem real em função da distância entre o objeto e a lente. Seu gráfico concorda com o resultado obtido no item ?
Passo 1
Então galera vamos lá!
A distância entre o objeto e sua imagem pode ser dada pela soma da distância do objeto até a lente e a distância da imagem até a lente, assim:
Agora usando a seguinte equação:
Vamos isolar , assim temos que:
Então temos que:
Agora vamos usar nossos conhecimentos de cálculo, vamos derivar essa expressão com respeito a e igular a zero para ver que valor de faz com que isso seja verdadeiro, pois assim teremos o valor de que minimiza essa expressão, depois é substitui-lo e encontrar .
O gráfico que temos que fazer em é justamente dessa expressão acima, só que como não temos um valor para a constante e o valor de que vamos encontra em vai depender dessa constante, vamos dividir todos os membros da expressão por , assim:
Então vamos fazer um gráfico .
Passo 2
Vamos lá então galera, vamos encontrar o menor valor de , temos o seguinte:
Fazendo , ficamos com:
Agora vamos igualar isso a zero encontrar , temos:
Temos que:
Substituindo na nossa expressão para , temos:
Então temos que o menor valor de é:
Passo 3
Agora vamos fazer o gráfico, temos:
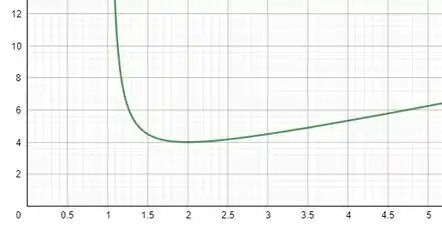
Se você reparar quando temos temos que mostrando que o gráfico concorda com nosso resultado.
Resposta