Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 111
111. Distância focal de uma lente zoom. A Figura mostra uma versão simples de uma lente zoom. A lente convergente possui distância focal e a lente divergente possui distância focal . As duas lentes estão separadas por uma distância variável que é sempre menor do que . O módulo da distância focal da lente divergente satisfaz à desigualdade . Para determinar a distância focal efetiva da combinação das duas lentes, considere um feixe de raios paralelos com raio entrando na lente convergente. Mostre que o raio do feixe diminui para o valor no ponto onde ele penetra na lente divergente. Mostre que à imagem se forma a uma distância à direita da lente divergente. Se os raios que emergem da lente divergente e atingem o ponto imagem final são prolongados para trás, para a esquerda da lente divergente, eles acabam atingindo o raio original em algum ponto . A distância entre a imagem final e o ponto é a distância focal efetiva da combinação das duas lentes; ou seja, se as duas lentes fossem substituídas por uma única lente situada no ponto com
distância focal , os raios paralelos incidentes seriam focalizados formando . Mostre que a distância focal efetiva é dada por . Sabendo que , e que a distância pode ser ajustada entre zero e , descubra a
distância focal máxima e a distância focal mínima para essa combinação. Qual é o valor da distância para obter ?
Passo 1
Então meu povo, borra lá!
Começando com o item , podemos encontrar o que é pedido fazendo uma semelhança de triângulos, das informações do enunciado conseguimos chegar a seguinte figura:
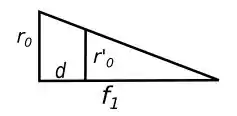
A base é em cima da lente convergente, a base é em cima da lente divergente e é a distância focal da lente convergente.
Para mostrar o que é pedido em temos que analisar o seguinte, a imagem que a primeira lente forma a sua direita a uma distância igual a serve como objeto para segunda lente a uma distância a esquerda da segunda lente tendo assim a formação da imagem a parti desse objeto.
O sinal de negativo é justamente porque o objeto está a esquerda da segunda lente.
A partir dessa análise e usando a seguinte equação vamos conseguir mostrar o que o enunciado quer.
Para o item vamos utilizar o mesmo método do item , semelhança de triângulos, já que se desenharmos a situação descrita em , teremos o seguinte:
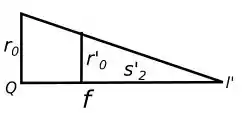
E para resolvermos o item basta pegar o que encontramos em e substituir os valores que o enunciado nos deu, aí é só da umas mexidinhas até encontrarmos o que queremos.
Passo 2
Vamos lá, como falei no passo o segredo é fazer a semelhança de triângulos, assim temos o seguinte:
Agora isolando , temos que:
Prontinho! Chegamos onde queríamos.
Passo 3
Vamos com tudo para o item agora, temos o seguinte do passo .
Utilizando a fórmula que mostrei no passo , temos o seguinte:
Agora para completar nossa demonstração vamos usar informação dada pelo enunciado sobre .
Então temos que:
Agora ajeitando para ficar igual a do enunciado, temos:
Prontinho meu povo!
Passo 4
Agora vamos a chegar na expressão pedida em , como falei no passo vamos fazer isso por semelhança de triângulos, assim:
Do desenvolvimento do item , nós podemos encontrar o seguinte:
Juntando essas duas informações temos que:
Agora usando o resultado do item , temos que:
Mais um item completo! Vamos para o próximo.
Passo 5
Agora para o item vamos pegar o resultado do passo anterior e usar os valores dados no enunciado.
Temos o seguinte:
Onde e e variando de a .
Agora vamos olhar a nossa fórmula, o único parâmetro variável é o e ele está no denominador, então quanto maior seu valor, menor será o de e quanto menor o seu valor, maior será o de .
Então temos que o valor máximo de ocorre em e o valor mínimo de ocorre em .
E a outra coisa que o item pede, basta isolar e substituir .
Vamos as contas, primeiro vamos encontrar o valor máximo de assim:
Agora o valor mínimo de , temos:
Agora vamos encontrar para , vamos lá!
Substituindo os valores que conhecemos, temos;