Um golfista arremessa uma bola a partir de uma elevação, imprimindo à bola uma velocidade inicial de e um ângulo de acima da horizontal. A bola atinge o campo a uma distância horizontal de do local do lançamento. Suponha que o campo seja plano. (a) Qual era a altura da elevação de onde foi arremessada a bola? (b) Qual era a velocidade da bola ao chegar ao campo?
Passo 1
Show de bolinhas galerinha, pra gente começar, precisamos lembrar da fórmula que dá a trajetória de um objeto lançado com um ângulo e uma velocidade inicial , expressa como:
O enunciado já diz os valores de e , e nosso objetivo é calcular a altura da elevação de onde a bola foi arremessada.
Passo 2
(a) Belezoca, então o enunciado diz que a bola toca o chão a uma distância horizontal de do local de lançamento, então a situação é a seguinte:
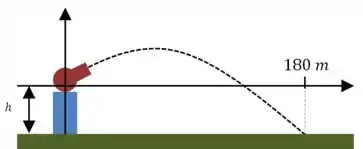
Para calcular na fórmula, só precisamos encontrar o valor de quando , logo:
Só que nesse caso tomamos a origemo do movimento como sendo o ponto onde a bola é lançada, ou seja, ela é lançada acima da altura inicial, de maneira que a altura é:
Passo 3
(b) A componente horizontal da velocidade é constante:
Logo
Mas a componente vertical muda com a aceleração da gravidade. Nós sabemos que no instante em que a bola passa pela altura do lançamento a sua velocidade tem o mesmo módulo da velocidade inicial, igual no desenho abaixo:

Então o módulo da componente vertical também deve ser o mesmo nessa altura:
Agora é só calcular o que acontece com a velocidade durante essa descida de sob acelerção , de acordo com a equação de Torricelli:
Sendo assim:
Passo 4
Então, logo antes de atingir o chão, a velocidade da bola tinha as seguintes componentes:
Para calcular o módulo dessa velocidade, podemos usar a relação:
Tal que:
Resposta
(a) A elevação de onde a bola foi arremessada tinha cerca de metros de altura.
(b) A bola chega ao campo com uma velocidade de .