Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 56
Um caiaquista precisa remar para o norte ao longo de um porto que tem 100 m de largura. A maré está subindo, criando uma corrente de maré que flui para leste a 2,0 m/s. O caiaquista consegue remar com rapidez de 3,0 m/s.
a. Em que direção e sentido ele deve remar a fim de deslocar-se em linha reta através do porto?
b. Quanto tempo ele levará para completar o trajeto?
Passo 1
Seguindo uma roda dos ventos simplificada com as direções norte (N), sul (S), leste (L) e oeste (O) podemos esquematizar os vetores
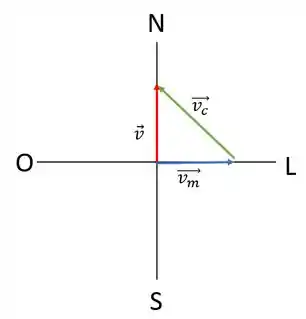
Em que é a velocidade da maré, é a velocidade que o caiaquista deve seguir e é o vetor resultante
E sabemos que a maré
A velocidade do caiaquista é
Passo 2
Como dá pra perceber na figura, ele tem que remar para do noroeste. Precisamos encontrar o ângulo. Para isso, vamos usar a trigonometria. Se considerar o ângulo indicado a baixo
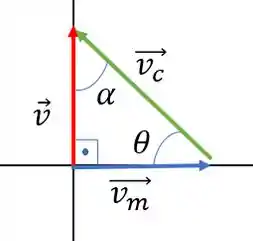
Temos que
Assim, se colocarmos os vetores
E o mesmo vale para
Assim, de norte para oeste possui 41,8 °
Passo 3
Para descobrir o tempo, vamos dar uma olhada em que o exercício nos dá: ele nos diz que o porto possui 100 m de largura! Então vamos usar para descobrir o tempo.
Substituindo na formulazinha
Assim, o tempo é 44,7 s!