Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 14.4 - Ex. 22a
14.22a. O tanque em forma de L mostrado na Fig. 14-36 está cheio d’água e é aberto na parte de cima. Se d=5,0m , qual é a força exercida pela água na face A?
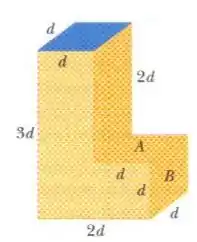
Passo 1
Então a gente tem um tanque mais ou menos assim
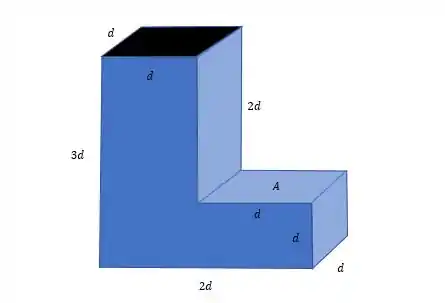
E a gente quer calcular a força na face “A” do tanque. Bom, a força pode ser calculada pela equação
O produto entre a pressão e a área.
Então primeiro a gente tem que calcular a pressão na altura que está a face “A”, para isso a gente pode usar a equação
Mas esse tanque está aberto em cima, então, a gente tem que somar a pressão atmosférica
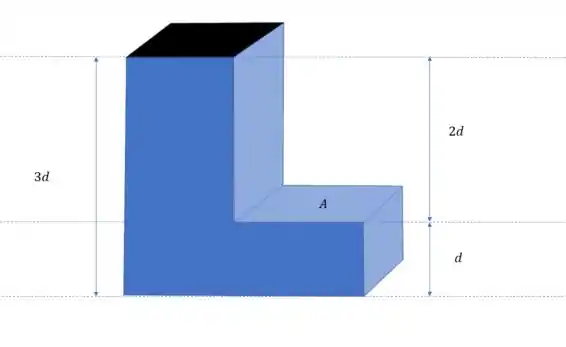
O tanque está cheio de água, e a densidade da água é , a pressão atmosférica é , e a ultima informação que a gente precisa é a altura, mas atenção essa altura não é a partir do solo, mas da superfície da água, que também é o topo da caixa, ou seja, . Vamos substituir esses valores na equação
Passo 2
Agora que a gente tem a pressão, a gente só precisa da área para calcular a força.
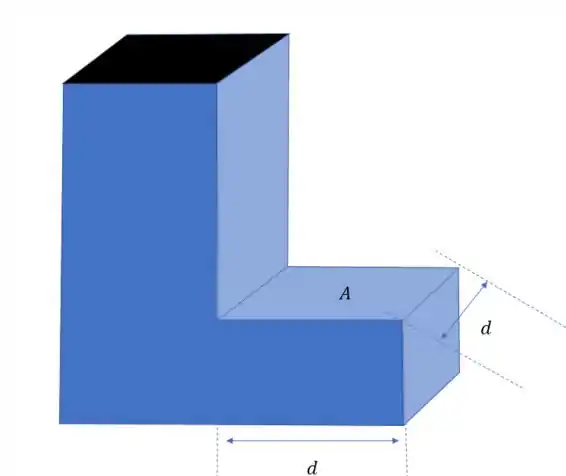
A face “A” é um quadrado, então, sua área é
Como , então
Passo 3
Só falta calcular a força agora.
Substituindo os valores