Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 18
Uma casca esférica está carregada eletricamente de forma homogênea. Utilize a lei de Gauss e considerações de simetria para demonstrar que o campo elétrico no interior da casca é nulo.
Passo 1
Vamos considerar uma casca esférica de raio com carga uniformemente distribuída e dentro dela vamos considerar uma superfície gaussiana esférica de raio :
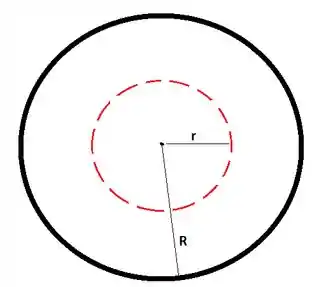
Pela lei de Gauss, temos que
Pela simetria do problema, o campo elétrico deve ser radial, de forma que
Além disso, como o campo deve depender apenas da distância , ele deve ser constante ao longo da superfície, de modo que ele sai da integral:
Passo 2
Com isso, a lei de Gauss nos dá:
Acontece que dentro dessa superfície esférica de raio não tem nenhuma carga, de modo que
Com isso, o campo dentro da casca esférica é nulo:
Resposta
Demonstração.