15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.
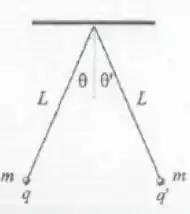
- Mostre que . (B) Imagine que um fino fio condutor faça contato simultâneo com as duas esferas e seja retirado após a redistribuição de cargas. Demonstre que o valor de aumenta, exceto se
Passo 1
Belezera galerinha, como as esferas estão suspensas no ar temos que a tração no fio devido ao peso , vai ser suficiente pra manter pra se opor a força peso e manter a carga suspensa. Devido a esse fato a tração também vai possuir uma componente tal que:
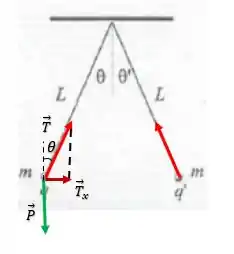
E pelo fato da tração se opor a força peso, temos:
Mas a componente na horizontal é dada por:
Logo:
Iradoso, e da mesma maneira a esfera do outro lado possui uma componente exatamente igual a essa, só que ao invés do ângulo ser , é , tal que:
Passo 2
Show de bolinhas, só que agora que começa a malandragem, porque como estamos falando de cargas elétricas, haverá uma força elétrica atuando sobre estas cargas. Essa força elétrica atua nas duas cargas em sentidos opostos, por exemplo na carga da esquerda a força é tal que:
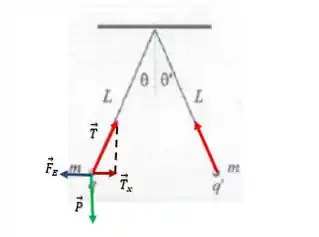
E se as esferas não estão se aproximando e nem se distanciando, temos que as forças que atuam na horizontal se anulam, de forma que:
Só que a força elétrica que uma esfera faz sobre a outra é igual para os dois lados, isto é, a força elétrica que esfera da esquerda aplica na esfera da direita é exatamente igual a força elétrica que a esfera da direita exerce sobre a esfera da esquerda, fazendo com que:
Logo:
E como nosso intervalo do ângulo está entre metade de da amplitude do pêndulo que equivale a um quarto de circunferência, isto é, . Logo teremos que tangentes com valores iguais dentro desse intervalo, tratam de ângulos iguais, portanto:
Passo 3
Show de bolinhas galera, uma maneira da gente provar que esse ângulo aumenta, é a gente mostrar que a distância também está aumentando:
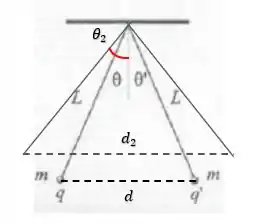
Saca só, na nossa imagem , e nesse caso também que a distância associada ao ângulo é menor do que a distância associada ao ângulo :
Ou seja, se a gente provar que depois da redistribuição de cargas as distâncias aumentaram, então também estaremos provando que o ângulo entre as cargas aumentou!!
Passo 4
Belezoca, agora que sabemos o passinho do malandro, podemos começar encontrando a distância .

Na figura abaixo podemos ver a distância dada como:
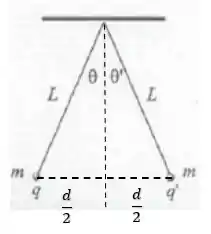
Tal que:
Logo:
Iradoso, outra coisa que também sabemos é que a força elétrica entre essas cargas, como vimos no Passo 2 é dada por:
Só que a fórmula da força elétrica é dada pela relação:
Dessa forma:
Só que a maciota master de todos os tempos aqui é que estamos tratando de cargas elétricas de esferas pontuais, MUUUUITO MUITO MUITO PEQUENAS, tal que essa distância entre elas também será muito pequena, levando o ângulo a ser extremamente pequeno chegando muito próximo de . E nessa situação, quando temos um ângulo muito muito muito próximo de , podemos fazer a seguinte aproximação:
Isso só vale para ângulo próximos a , por exemplo e , dessa forma nossa relação entre as forças se transforma em:
E vimos agorinha que , logo:
Passo 5
Belejóia, no primeiro momento, temos que as cargas são e , dessa forma a distância inicial é:
Já a distância vai ser dada após a redistribuição de cargas devido a conexão do fio condutor. Depois de redistribuição, as cargas serão divididas igualmente de forma que:
Logo é:
E pra saber qual dessas distâncias é maior, podemos analisar a razão entre elas, isto é , se essa razão for maior que , então . Se a distância for exatamente , quer dizer e sobretudo se a razão for menor que , então teremos que . Dito isso, fazemos que:
Se a gente cancelar os termos que se repetem em cima e embaixo, teremos que:
Agora temos que é o nosso numerador, enquanto é o nosso denominador. Vamos chamar da nossa função diferença entre esses termos:
E o legal dessa função é que se quer dizer que o numerador vai ser maior que o numerador tal que . E da mesma forma se essa função quer dizer exatamente o contrário, e nosso numerador vai ser menor que o denominador levando . E se , o denominador será exatamente igual ao numerador e nossa razão será . Só que descobrimos que nossa função é uma forma quadrática, dada por:
E pra quem pensou que nunca mais ia usar álgebra na vida rsrs... Tá superamos, então para formas quadráticas, podemos verificar a existência de valores negativos, positivos ou iguais a zero decompondo em forma de matriz, desse jeito:
Então para nossa forma quadrática temos:
E se a gente calcular os autovalores dessa função, veremos que são e
Portanto, nossa função só assume valores positivos ou iguais a zero, tal que:
E por exemplo se teremos que:
Ou seja, se a as cargas forem iguais, a distância vai permanecer a mesma. Mas qualquer outro caso que acontece, fará com que , e portanto, a distância final será maior que a inicial.
Resposta
- Demonstração.
- Demonstração.