Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 24

Uma partícula com carga q situa-se sobre o eixo de um disco circular de raio a , à distância b do mesmo, como mostra a Figura 15.21. Calcule o fluxo do campo elétrico no disco. Sugestão: considere uma casca esférica centrada na carga e passando pelo contorno do disco.

Passo 1

Seguindo a sugestão do enunciado, podemos considerar uma esfera centrada na carga q que contorne o disco:

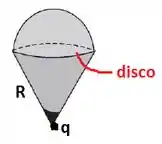
O fluxo do campo elétrico sobre o pedacinho da calota esférica é igual ao fluxo sobre o disco pois todas as linhas de campo que atravessam o disco vão atravessar também a calota esférica:

Φ d i s c o = Φ c a l o t a   e s f e r i c a

O fluxo sobre a calota esférica é tranquilo de calcular pois o campo da carga pontual é radial e dado por

E = 1 4 π ϵ 0 q R 2

Daí, o fluxo sobre a calota será

Φ c a l o t a   e s f e r i c a = ∫ E → ⋅ d A → = ∫ 1 4 π ϵ 0 q R 2   d A = 1 4 π ϵ 0 q R 2 ∫ d A = 1 4 π ϵ 0 q R 2 ⋅ A c a l o t a

Lembre-se que

R 2 = a 2 + b 2

Passo 2

Precisamos da área da calota esférica:

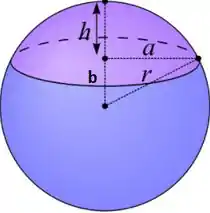
Eu dei uma pesquisada no wikipedia e achei:

A c a l o t a = 2 π R h

Mas sabemos que

h = R - b

Logo,

A c a l o t a = 2 π R R - b

Com isso, o fluxo sobre a calota será

Φ c a l o t a   e s f e r i c a = 1 4 π ϵ 0 q R 2 ⋅ 2 π R R - b

Φ c a l o t a   e s f e r i c a = q 2 ϵ 0 ⋅ R - b R = q 2 ϵ 0 1 - b R

Por fim, usando R = a 2 + b 2 :

Φ c a l o t a   e s f e r i c a = q 2 ϵ 0 1 - b a 2 + b 2

Como visto no começo do problema, o fluxo sobre a calota é igual ao fluxo sobre o disco, de modo que

Φ d i s c o = q 2 ϵ 0 1 - b a 2 + b 2

Resposta

Φ d i s c o = q 2 ϵ 0 1 - b a 2 + b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cubo possui uma aresta de comprimento L = 0,300m . Ele é colocado com um cértice na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, mas é dado por E → = ( - 5,0N / C ∙ m ) x i
No Exemplo 21.11 (Seção 21.5 ), verificamos que o campo elétrico produzido por um fio retilíneo infinito carregado é perpendicular ao fio e possui módulo E = λ / 2 π ϵ 0 r . Considere uma superfície c
No Exemplo 21.11 (Seção 21.5 ), verificamos que o campo elétrico produzido por um fio retilíneo infinito carregado é perpendicular ao fio e possui módulo E = λ / 2 π ϵ 0 r . Considere uma superfície c
O cubo na Figura 22.32 possui uma aresta L = 10,0c m . O campo elétrico é uniforme, paralelo ao plano x y , formando um ângulo de 36,9 ° medido do eixo + O x para o eixo + O y , e possui módulo E = 4,
Um cubo possui uma aresta de comprimento L = 0,300m . Ele é colocado com um vértice na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, mas é dado por E → = ( - 5,0N / C ∙ m ) x i