Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 22

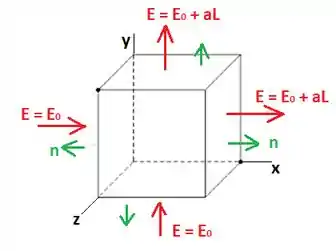
A Figura 15.19 mostra a projeção de um cubo no plano x y . (a) Na região ocupada pelo cubo, o campo elétrico tem a forma E → = E 0 + a x   i → , em que E 0 e a são constantes. Calcule a carga líquida dentro do cubo. (b) Refaça o cálculo da carga supondo o campo na forma E → = E 0 + a x i → + E 0 + a y j → .

Passo 1

Nesse problema nós conhecemos o campo elétrico e vamos usá-lo para achar a carga líquida dentro do cubo pela lei de Gauss:

∮ E → ⋅ d A → = q i n t ϵ 0

No item (a) o campo elétrico temo componentes apenas na direção x , de modo que devemos considerar apenas duas faces para calcular o fluxo:

Numa das faces, no plano x = 0 , o campo é E = E 0 , enquanto na outra face em x = L ele é E = E 0 + a L . Note que esses campos são constantes nas faces. Além disso, temos que adotar o versor normal n ^ apontando para fora do cubo.

Na primeira face o fluxo será negativo:

Φ E 1 = ∫ E 0 i → ⋅ - i →   d A = - E 0 ∫ d A = - E 0 L 2

Já na segunda face:

Φ E 2 = ∫ E 0 + a L i → ⋅ i →   d A = E 0 + a L L 2

Como as demais faces não contribuem para o fluxo, temos que

∮ E → ⋅ d A → = - E 0 L 2 + E 0 + a L L 2 = a L 3

Logo,

a L 3 = q i n t ϵ 0 → q i n t = ϵ 0 a L 3

Passo 2

No item (b) nós adicionamos uma nova componente para o campo elétrico na direção y :

É fácil perceber que as contas paras essas novas duas faces vão ser idênticas ao que fizemos no passo 1, de modo que

∮ E → ⋅ d A → = 2 a L 3

Daí,

2 a L 3 = q i n t ϵ 0 → q i n t = 2 ϵ 0 a L 3

Resposta

q i n t = ϵ 0 a L 3

q i n t = 2 ϵ 0 a L 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma linha longa que possui densidade linear de carga uniforme + 50,0μ C / m corre paralelamente à superfície de uma placa de plástico plana e grande, a 10,0c m de distância, e que possui uma densidade
O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni
O campo elétrico E → na Figura 22.35 é paralelo ao eixo O x em todos os pontos da região, portanto os componentes E y e E z são nulos. O componente x do campo elétrico E x depende de x , mas não depen
Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca
Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde