Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 43
Na figura 28-45, um bastão condutor de massa e resistência desprezível está livre para deslizar sem atrito ao longo de dois trilhos paralelos que têm resistências desprezíveis, estão separados por uma distância e conectados por uma resistência . Os trilhos estão presos a um longo plano inclinado que faz um ângulo com a horizontal. Há um campo magnético apontando para cima, como mostrado. (a) Mostre que há uma força retardadora dirigida para cima no plano inclinado dada por . (b) Mostre que a rapidez terminal do bastão é dada por .
Passo 1
Falaaa meu povo.
A figura abaixo mostra o diagrama de forças do nosso sistema.
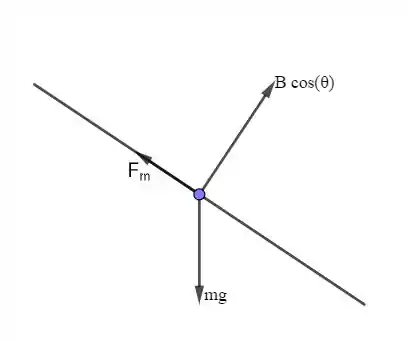
O importante a se notar é o seguinte: conforme a barra começa a cair, uma fem do movimento surge, dada por
Note que tomamos apenas a componente do campo magnético normal ao plano inclinado, pois a componente tangencial não consegue produzir nenhuma fem do movimento.
Dessa maneira, uma corrente surge, de tal forma que a componente do campo magnético faz uma força , onde é a corrente que passa pelo circuito.
Em resumo, há basicamente duas forças atuando na direção do movimento no corpo:
- que é a força magnético;
- que é a componente do peso.
Passo 2
- Da discussão acima, vimos que
- A velocidade terminal é atingida quando a força magnética igualar a força peso. A partir daí, a barra não terá mais nenhuma aceleração. Logo,
que é o que queríamos mostrar.
Bem, é isso galerinha :D
Resposta
- Demonstração.
- Demonstração.