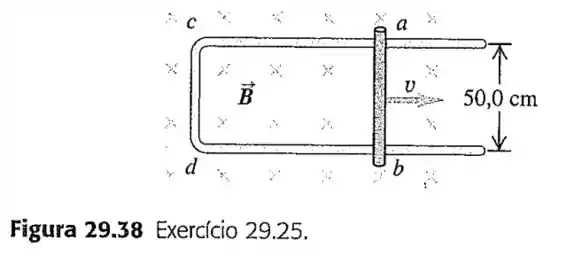
25- Na Figura , uma barra condutora está em contato com os trilhos e . O dispositivo encontra-se em um campo magnético uniforme de perpendicular ao plano da figura.

Calcule o módulo da fem induzida na barra quando ela se desloca da esquerda para a direita com velocidade igual a .

Em que sentido a corrente flui na barra?

Sabendo que a resistência do circuito é igual a (supostamente constante), determine o módulo, a direção e o sentido da força necessária para manter a barra se deslocando da esquerda para a direita com velocidade de . Despreze o atrito.

Compare a taxa do trabalho mecânico realizado pela força magnética a taxa da energia térmica dissipada no circuito .

Como a resistência dessa barra é de então a corrente induzida é de:

Note que só surge corrente induzida pois a área aumenta, se fosse somente a barra, o fluxo magnético não aumentaria.

Então a força magnética que surge na barra é de:

Como e são perpendiculares então , logo:

Pela regra da mão direita temos que a corrente induzida que aponta para cima no plano, e o campo magnético que aponta no sentido de entrar na folha cria uma força magnética que aponta para a esquerda, então para a barra se deslocar para a direita temos que ter essa mesma intensidade de força porém para direita.

A energia dissipada no circuito é de:

E a potência mecânica :

As duas energias são iguais, que vai de encontro com a conservação de energia de um sistema. Lindo né?