1.77 Uma artista está criando um novo logotipo para a página de sua companhia na Internet. No programa gráfico que ela está usando, cada pixel em um arquivo de imagem possui coordenadas (x, y), onde a origem (0, 0) está situada no canto superior esquerdo da imagem, o eixo +Ox aponta para a direita e o eixo +Oy aponta para baixo. As distâncias são medidas em pixels. a) A artista desenha uma linha ligando o local do pixel (10, 20) com o local (210, 200). Ela deseja desenhar uma segunda linha que começa em (10, 20), tem comprimento de 250 pixels e forma um ângulo de 30° medido no sentido dos ponteiros do relógio a partir da direção inicial. Qual o local do pixel no qual esta segunda linha deve terminar? Dê a resposta com os algarismos significativos do pixel indicado. b) A artista desenha agora uma flecha ligando a extremidade direita inferior da primeira linha com a extremidade direita inferior da segunda linha. Determine o módulo e a direção desta flecha. Faça um diagrama mostrando as três linhas.
Passo 1
Vamos lá, meu povo! A questão tá dizendo que a artista fez uma linha que foi do pixel (10,20) até o (210,200) e depois pegou uma outra linha, que fez 30° com a linha anterior e andou 250 pixels. A questão ao agora quer saber qual o local do pixel, ou seja, o (x,y) que essa linha vai terminar.
Primeiro a gente vai ter que achar o ângulo que a primeira linha faz com os eixos x e y pra depois encontrar o ângulo real da segunda linha e assim encontrar as componentes dela.
Ficou curioso(a)? Então vamos lá \O/.
Passo 2
Pra encontrar o ângulo da primeira linha com o eixo Ox, vamos usar a tangente. Lembrando que o valor de x é (210-10) e que o valor de y é (200-20):
Agora a gente usa o arco-tangente pra achar o ângulo:
Agora que a gente tem o ângulo a linha 1 faz com o eixo Ox, é só somar com os 30° graus que a linha 2 faz com a 1 e temos que o ângulo que a linha 2 faz com o eixo Ox é de 72°.
Agora bora o valor das componentes.
Passo 3
Pra saber o valor de é só somar os 10 da posição inicial com o módulo (250) multiplicado pelo cosseno do ângulo. Vejamos:
Seguimos com o mesmo raciocínio em y, só que agora usando o seno:
Agora sabemos que o pixel que a linha vai terminar é o pixel (87,258).
Bora pro item b) que isso aqui tá bonito!
Passo 4
Agora a questão quer saber o módulo e a direção de uma flecha que liga a extremidade da linha 1 com a extremidade da linha 2.
Pra saber o módulo dessa flecha é só usar o maravilindo Teorema de Pitágoras, sabendo que o x dessa flecha é igual ao x da linha 1 menos o x da linha 2 e que o y da flecha é o y da linha 1 menos o y da linha 2.
Pra achar o ângulo com o eixo Ox vamos usar a tangente.
Então bora!
Passo 5
Vamos usar Pitágoras para achar o módulo:
Uhuu! Temos o módulo. Agora vamos achar o ângulo.
Passo 6
Sabendo que a tangente do ângulo que a flecha faz com o eixo x é , tiramos o arco-tangente desse valor e encontramos o ângulo. Simbora!
O ângulo é negativo porque ele segue no sentido anti-horário enquanto o sentido positivo é o sentido horário.
Passo 7
Agora podemos desenhar o diagrama da seguinte maneira:
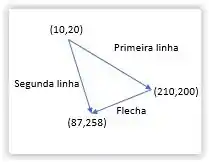
E agora sim... Ufa! Acabamos! XD
Resposta
- (87,258)
- Módulo: 136; Direção: -25° em relação ao eixo Ox.