Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.9 - Ex. 47
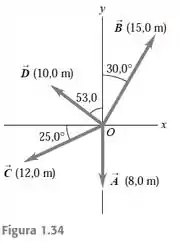
Escreva cada vetor indicado na Figura 1.34 em termos dos vetores unitários e .
Passo 1
Oi, galerinha!
Nessa questão o que o enunciado está pedindo é para decompormos as componentes em termos e de todos os vetores da figura!
Para isso vamos usar a relação com seno para componente em e cosseno para componente em .
Veja só! 😊
Passo 2
Então vamos decompor as componentes:
Para o vetor
Para o vetor
Para o vetor
Para o vetor
Tranquilo até aqui? 😎
Passo 3
Agora vamos somar suas componentes para obter os respectivos vetores resultantes:
E aí! entendeu tudo? Responde Aí! 😉
Resposta
Exercícios de Livros Relacionados
O vetor A → tem um módulo de 12,0m e faz um ângulo de 60,0° no sentido anti-horario com o semi eixo positivo x de um sistema de coordenadas xy. O vetor B → é dado por 12,0m i ^ + 8,00m j ^ no mesmo si
Determine a soma dos quatro vetores a seguir (a) em termos dos vetores unitários e em termos (b) do módulo e (c) do ângulo em relação ao semi-eixo x positivo. P → : 10,0m . 25,0 °sentidoanti-horárioem
Uma partícula sofre três deslocamentos sucessivos em um plano: d → 1 ,4,00m para sudoeste, d → 2 ,5,00m para leste e d → 3 ,6,00m em uma direção 60,0 ° no norte do leste. Use um sistema de coordenadas
Dois vetores a → e b → têm componentes, em metros, a x = 3,2 , a y = 1,6 , b x = 0,5 e b y = 4,5 . (a) Determine o ângulo entre a → e b → . Existem dois vetores no plano x y que são perpendiculares a
Em um jogo de futebol, a bola está inicialmente no centro do campo. Considere um sistema de coordenadas O x y no plano do campo e cujo centro O coincida com o centro do campo. Depois do primeiro chute