Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 72a

1.72 - a) Ache o módulo e a direção do vetor R → que é a soma dos três vetores A → ,   B →   e   C → e indicados na Figura 1.34. Desenhe um diagrama para mostrar como é formado com esses três vetores.

Passo 1

Pra achar o módulo, a gente vai ter que decompor os comprimentos em x e em y e depois usar o teorema de Pitágoras com R x   e   R y .

Passo 2

Vamos lá, decompor os comprimentos! Começando por x:

R x = A x + B x + C x

R x = 0 + 15 s e n 30 ° - 12 c o s 25 °

R x =   - 3,4 m

E agora y:

R y = A y + B y + C y

R y = -   8 + 15 c o s 30 ° - 12 s e n 25 °

R y = - 0,08 m

Passo 3

Agora vamos achar o módulo por Pitágoras:

R = - 3,4 2 + - 0,08 2

R = 3,4 m

Achamos o módulo!! Só falta achar o ângulo pra depois desenhar o diagrama bonitinhos.

Passo 4

Como as duas componentes de R → são negativas, isso significa que esse vetor está no terceiro quadrante. Então queremos saber o ângulo que ele faz com o eixo -Ox e pra isso vamos usar o método da tangente:

t g α = R y R x =   - 0,08 m - 3,4 m = 0,024

Agora tiramos o arco-tangente desse valor pra encontrar o ângulo:

a r c t g 0,024 =   1,4 °

Passo 5

Agora o diagrama:

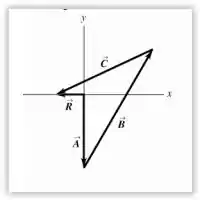
Aeh! Terminamos!

Resposta

Módulo: 3,4m

Direção: 1,4 ° com o eixo -Ox

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja A → = 5 i ^ + 2 j ^ e B → = - 3 i ^ - 5 j ^ e D → = A → - B → Expresse o vetor D → em termos de componentes.Desenhe um sistema de coordenadas e sobre ele represente os vetores A → , B → e D → .Qu
A posição de uma partícula em função do tempo é dada por r → = 5,0 i ^ + 4,0 j ^ t 2 m , onde t está em segundos.Qual é a distância da partícula em relação à origem em t = 0 ,2 e 5s ?Obtenha uma expre
Seja A → = 5 i ^ + 2 j ^ e B → = - 3 i ^ - 5 j ^ e E → = 2 A → + 3 B → Expresse o vetor E → em termos de componentes.Desenhe um sistema de coordenadas e sobre ele represente os vetores A → , B → e E →
Carlos corre com velocidade v → = ( 5,0m / s ,25 °n o r d e s t e ) durante 10 minutos. A que distância ao norte de seu ponto de partida Carlos terminará?
Obtenha um vetor com a mesma orientação que o vetor ( i ^ + j ^ ) e com módulo igual a 1.