Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 9.Problemas - Ex. 3
Em 1831, Michael Faraday fez girar um disco de cobre sobre os polos de um imã em forma de ferradura e observou o aparecimento de uma diferença de potencial constante entre duas escovas, uma em contato com o eixo do disco e a outra na periferia. Seja o raio do disco.
- Se o disco gira com velocidade angular , com seu plano perpendicular ao campo magnético uniforme , qual é a diferença de potencial gerada entre o eixo e a periferia?
- Devido a esta diferença de potencial, passa uma corrente entre o eixo e a periferia. Calcule o torque que é necessário exercer para manter o disco girando e mostre que a potência fornecida é igual a potência gerada.
Passo 1
Para começar, podemos fazer um esboço da configuração que o problema nos dá.
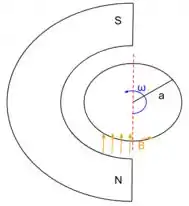
Agora vamos levar em consideração que o fluxo do campo magnético é dado por
E o campo B no interior é constante. A sacada aqui é perceber estamos falando de um disco. Sabendo que o raio é , portanto o arco é
e a área será
Então o fluxo será
Sabendo que
e lembrando que
Temos
Passo 2
No item (b) ele pede o torque. Precisamos lembrar que
E que a força magnética é
Já sabemos que B é constante e =. Agora só precisamos fazer a integral abaixo
Passo 3
Agora vamos verificar as potências geradas e fornecidas?!
Primeiro, temos que a potência fornecida é dada por
Para terminar, a potência gerada é
Como você pode ver, as potências são iguais.