Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 11d
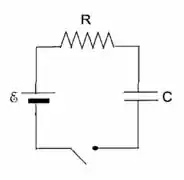
No circuito da figura, a chave é ligada em , como capacitor descarregado.
- Obtenha a energia total dissipada no resistor durante esse tempo. Mostre que a metade da energia fornecida estará armazenada no capacitor e a outra metade dela terá sido dissipada no resistor.
Passo 1
Vamos lá!
Temos que potência dissipada no resistor é dada por
Bom como queremos saber a energia no capacitor quando , temos que integrar
Passo 2
Como a corrente neste circuito decai exponencialmente, onde
e temos
Resposta
Exercícios de Livros Relacionados
Que múltiplo da constante de tempo τ é o tempo necessário para que um capacitor inicialmente descarregado seja carregado com 99,0% da carga final em um circuito RC série?
Um capacitor com uma carga inicial q 0 é descarregado carregado através de um resistor. Que múltiplo da constante de tempo τ é o tempo necessário para que o capacitor descarregue (a) um terço da carga
Em um circuito RC série, ε = 12,0 V , R = 1,40 M Ω e C = 1,80 μ F . (a) Calcule a constante de tempo. (b) Determine a carga máxima que o capacitor pode receber ao ser carregado. (c) Qual é o tempo nec
A Fig. 27-64 mostra o circuito de uma lâmpada piscante como as que são usadas nas obras de estrada. Uma lâmpada fluorescente L (de capacitância desprezível) é ligada em paralelo com o capacitor C de u
Na Fig. 27-66, R 1 = 10,0 k Ω , R 2 = 15,0 k Ω , C = 0,400 μ F e a bateria ideal tem uma força eletromotriz ε = 20,0 V . Primeiro. A chave é mantida por um longo tempo na posição fechada. até que seja