Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 7.2 - Ex. 19
A constante de uma certa mola de massa desprezível é dada por . a) Qual deve ser a distância da compressão dessa mola para que ela armazene uma energia potencial igual a
? b) Você coloca verticalmente uma das extremidades da mola sobre o solo. Deixa cair sobre a mola um livro de a partir de uma altura de acima da extremidade superior da mola. Calcule a distância da compressão máxima dessa mola.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a distância da compressão máxima da mola, sabendo que ela tem constante e energia potencial igual a e que foi colocado sobre a mola um livro de a partir de uma altura de acima de sua extremidade superior.
Nessa questão, vamos usar os métodos de energia. Há mudanças na energia potencial elástica e gravitacional. E sabemos que a energia elástica é dada por:
E a energia potencial gravitacional é dada por:
O trabalho é , pois apenas o trabalho é feito por gravidade e força da mola. Então, vamos encontrar a distância usando essas fórmulas. Vamos lá!
Passo 2
a) Então, de
Chegamos que:
E substituindo os valores, obtemos:
Passo 3
b) Vamos ilustrar o ponto , e o ponto :
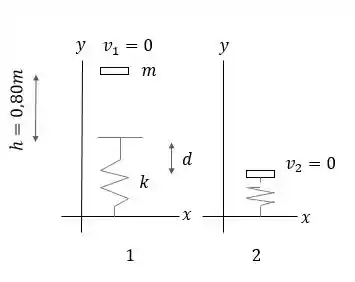
O que nos dá:
Como ficamos com:
e
Também, na posição final.
Passo 4
Na posição , teremos:
Na posição , temos:
Substituindo isso no balanço de energia visto no passo anterior, ficamos com:
A energia potencial gravitacional original do sistema é convertida em energia potencial do compressor da mola.
Isso implica que:
Como deve ser positivo, então:
Subtituindo os valores, isso implica que:
Valeu, galera! Até a próxima! 😉