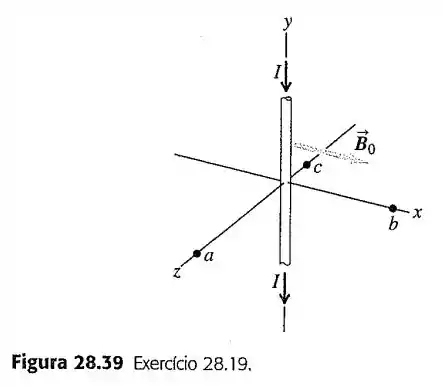
19- Um fio retilíneo longo está situado sobre o eixo e conduz uma corrente no sentido (Figura ). Além do campo magnético produzido pelo fio, existe um campo magnético uniforme com módulo igual a apontando no sentido . Calcule o módulo, a direção e o sentido do campo magnético total nos seguintes pontos sobre o plano :

Agora para a letra nós temos o campo magnético causado pela corrente igual a:

Então a soma dos dois campos nos dará:

Cujo módulo desse campo será de:

E o sentido desse campo será de:

Para a letra :

Logo a soma dos dois campos magnéticos serão de:

Logo a magnitude do campo será de:

Com sentido em