Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 91b
Os dois vetores e são desenhados a partir de um mesmo ponto e b) Mostre que quando , o ângulo entre os vetores é maior do que 90°.
Passo 1
Olá, galerinha!
Nessa letra b, vamos por partes. Para mostrar essa afirmação, vamos ter que usar a relação
Sendo que é o ângulo entre .
Vamos analisar então a equação!
Bora lá!
Passo 2
Perceba que, para ser menor que , tem que ser menor que , e isso só é possível quando .
E olhando para o círculo trigonométrico, vemos que isso acontece para valores maiores que e menores que .
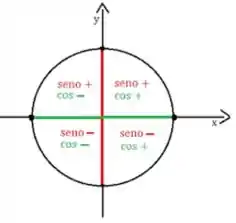
Como o enunciado diz, quando , o ângulo entre os vetores é maior do que 90°.
Então o enunciado foi verdadeiro de novo! XD
Vamos pra próxima! Responde Aí!
Resposta
Exercícios de Livros Relacionados
Determine os ângulos entre os vetores A → e B → dados: (a) A → = 3 i ^ - 6 j ^ , B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Determine A → ∙ B → para os seguintes vetores: (a) A → = 3 i ^ - 6 j ^ ,B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Determine os ângulos entre os vetores A → e B → dados: (a) A → = 3 i ^ - 6 j ^ , B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Determine A → ∙ B → para os seguintes vetores: (a) A → = 3 i ^ - 6 j ^ ,B → = - 4 i ^ + 2 j ^ ; (b) A → = 5 i ^ + 5 j ^ ,B → = 2 i ^ - 4 j ^ ; (c) A → = 6 i ^ + 4 j ^ ,B → = 4 i ^ - 6 j ^ ;
Uma partícula de 2,0 kg sofre um deslocamento de Δ r → = 3,0m i ^ + 3,0m j ^ + - 2 , 0m k ^ . Durante esse deslocamento, uma força constante F → = 2 , 0N i ^ - 1 , 0N j ^ + 1 , 0N k ^ atua sobre a par