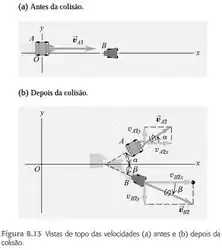
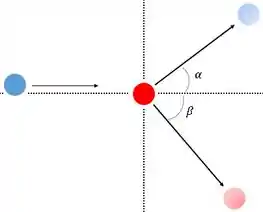
Um próton se deslocando ao longo do eixo com velocidade sofre uma colisão elástica fora da linha central com outro próton idêntico que está inicialmente em repouso. Depois desse impacto, o primeiro próton se desloca com velocidade no primeiro quadrante, formando um ângulo com o eixo , e o segundo próton se desloca com velocidade no quarto quadrante formando um ângulo com o eixo (veja a Figura 8.13). a) Escreva as equações que descrevem a lei da conservação do momento linear para os componentes x e y. b) Eleve ao quadrado as equações obtidas na parte (a) e some membro a membro os resultados. c) Introduza agora o fato de a colisão ser elástica. d) Demonstre que . (Você está demonstrando que esse resultado é válido para qualquer colisão elástica fora da linha central entre dois corpos de mesma massa, quando um dos corpos está inicialmente em repouso.)

a) Vamos separar em dois momentos nossas contas. Primeiramente em e posteriormente em .

Para temos que de início a partícula azul se desloca para a direita com velocidade enquanto a partícula vermelha repousa sobre a origem do sistema.

Desta forma, podemos escrever a conservação de momento em como sendo

Pela decomposição das velocidades, temos que

e

Da mesma forma para teremos que inicialmente as duas partículas estão em repouso sobre essa coordenada, ou seja, .

Assim, temos que

Onde .

b) Vamos elevar ao quadrado a primeira equação em , ficando com:

E para teremos:

Somando ambas as equações e usando as seguintes relações trigonométricas

e

Ficamos com:

c) O fato da colisão ser elástica diz que toda energia inicial será igual a energia final, ou seja

Subtituindo na equações encontrada no item c) temos que:

d) Implicando que

Valeu, galera! Até a próxima! 😉