Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 93b
1.93b Um cubo é colocado de modo que um dos seus vértices esteja na origem e três arestas coincidam com os eixos , e de um sistema de coordenadas (Figura 1.43). Use vetores para calcular b) o ângulo entre a linha ac (a diagonal de uma das faces) e a linha ad.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um cubo é colocado de modo que um dos seus vértices esteja na origem e três arestas coincidam com os eixos , e de um sistema de coordenadas da seguinte forma:
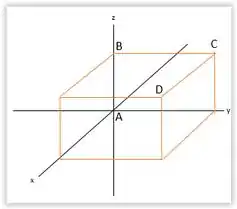
Bom... pelo que colocamos na letra a), as arestas do cubo têm módulo igual a .
Nessa questão queremos saber o ângulo entre a linha () que vamos chamar de e está definida nos eixos e positivos, e a linha (), que vamos chamar de e está definida em todos os eixos positivos.
E aí?? Bora lá?? 😉
Passo 2
Primeiro temos que saber os módulos de e de .
Começando por , aplicando os vetores unitários, temos:
Agora , aplicando os vetores unitários, temos:
Passo 3
O próximo passo é usar a equação 1.27 para encontrar o produto escalar entre e . Só vamo:
Passo 4
Agora é só substituir esse resultado na equação 1.18 pra encontrarmos o ângulo:
E é só fazer aquele arco-cosseno maroto:
Achamos o ângulo!! 😉