Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 87a

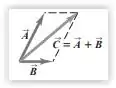
1.87a - A Figura 1.11c mostra um paralelogramo cujos lados são os vetores e a) Mostre que o módulo do produto vetorial destes vetores é igual à área deste paralelogramo. (Sugestão: área base altura.)

Passo 1

Se formos pensar em termos de área, o vetor é a base do paralelogramo e o vetor é altura do paralelogramo. Pra achar a área a gente só precisa do módulo desses vetores.

Supondo que os vetores e estão no plano xy, achar a área entre eles é o mesmo que achar a área entre a componente x do vetor e a componente y do vetor , sendo que deixamos o vetor paralelo ao eixo x.

Então bora, pimpolhos!

Passo 2

Sabemos que , pois o vetor está paralelo ao eixo x. Sabemos também que a componente y do vetor é , sendo que é o ângulo entre os vetores e .

Então temos:

Como o produto vetorial entre e é , mostramos que a área do paralelogramo é igual ao produto vetorial entre e .

Bora pra próxima!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1.90 Ângulo da ligação no metano. Na molécula do metano, CH4, cada átomo de hidrogênio ocupa o vértice de um tetraedro regular em cujo centro se encontra o átomo de carbono. Usando coordenadas de tal

1.88 O vetor A → possui comprimento de 3,50 cm e aponta para o interior desta página. O vetor B → aponta do canto direito inferior desta página para o canto esquerdo superior desta página. Defina um s

b)Prove que os dois vetores são anticomutativos para o produto vetorial; ou seja, prove que A → × B → = - B → × A → .

Ache o ângulo entre cada par de vetores:c) A → = - 4,0i ^ + 2,0j ^ e B → = 7,0i ^ + 14,0j ^ ;

Para os vetores indicados na Figura 1.35, a) ache o módulo e a direção do produto vetorialA → × B → ; b) ache o módulo e a direção do produto vetorial B → ×A → .