Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Exercício - Ex. 49

21.49 Em um sistema de coordenadas ortogonais, uma carga puntiforme positiva q =   6,0 ⋅   10 - 9   C é colocada no ponto x = + 0,150   m , y = 0 , e outra carga idêntica é colocada no ponto x = - 0,150   m , y = 0 . Estabeleça os componentes x   e   y , bem como o módulo, a direção e o sentido do campo elétrico nos seguintes pontos: ( a ) a origem; b   x = 0,300   m , y =   0 ; c x = 0,150   m ,   y = - 0,400   m ;   d x =   0 ,   y = 0,200   m

Passo 1

Vamos aplicar:

E = 1 4 π ϵ 0 ⋅ q r 2

E = k ⋅ q r 2

s e n d o   k = 8,988 ⋅ 10 9   N ⋅ m 2 C 2

Um esquema para o problema é:

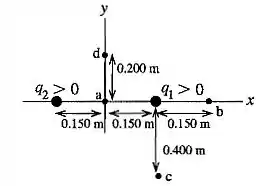
Passo 2

a

As duas cargas são idênticas e estão equidistantes logo nessa letra o E = 0 , observe:

E = E 2 - E 1

E = k ⋅ q r 2 - k ⋅ q r 2

E = 8,988 ⋅ 10 9 ⋅   6,0 ⋅   10 - 9 ( 0,150 ) 2 - 8,988 ⋅ 10 9 ⋅   6,0 ⋅   10 - 9 ( 0,150 ) 2

E = 0

E x = 0

E y = 0

Passo 3

(b)

Nessa o campo elétrico só existirá no eixo x , veja os vetores em b:

E = E 1 + E 2

E 1 = k ⋅ q r 2 = 8,988 ⋅ 10 9   ⋅   6,0 ⋅   10 - 9 0,150 2 = 2396,8   N / C

E 2 = k ⋅ q r 2 = 8,988 ⋅ 10 9   ⋅   6,0 ⋅   10 - 9 0,450 2 = 266,3 N C

E = 2663,1 N / C ,   n a   d i r e ç ã o   d e + x

E x =   2663,1   N / C

E y = 0   N / C

Passo 4

(c)

Nessa a gente vai ter que usar nossos dotes de trigonometria, o esquema será:

Já tiramos:

Assim:

E 1 = k ⋅ q r 2 = 8,988 ⋅ 10 9   ⋅   6,0 ⋅   10 - 9 0,4000 2 = 337,1 N / C

E 1 x = 0             &             E 1 y = - E 1 = - 337,1 N / C

E 2 = k ⋅ q r 2 = 8,988 ⋅ 10 9   ⋅   6,0 ⋅   10 - 9 0,500 2 = 215,7 N / C

E 2 x = + E 2 ⋅ C o s θ = + 129,4   N / C                 &               E 2 y = - E 2 ⋅ s i n ⁡ ( θ ) = - 172,6 N / C

Juntando:

E x = E 1 x + E 2 x = + 129,4   N / C

E y = E 1 y + E 2 y = - 509,7   N / C

Então o E total será:

E =     E x 2 + E y 2         ≅ 526   N / C

Para achar a orientação do E total podemos usar o E x e o E y , como na imagem a seguir...

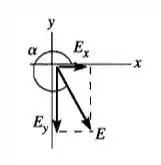
Cuidando para não confundir E com E 2 , E x com E 2 x e E y com E 2 y da imagem do passo 3.

Então podemos desenvolver:

tan ⁡ α = E y E x

tan ⁡ α = - 509,7 129,4 ≅ - 3,953

⇒ α = 284 ° ,   a n t i - h o r a r i o   d e + x  

Passo 5

(d)

Nessa situação o esquemático vai ser:

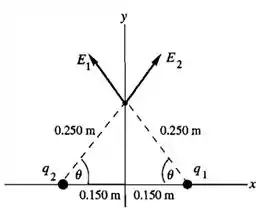
Deduzimos:

s i n θ = 0,200 0,250 = 0,8  

No ponto analisado a decomposição será:

Temos:

E 1 = E 2 = k ⋅ q r 2 = 8,988 ⋅ 10 9   ⋅   6,0 ⋅   10 - 9 0,250 2 = 862,8   N / C

E 1 x = - E 1 cos ⁡ θ     &   E 2 x = + E 2 cos ⁡ θ    

E x = E 1 x + E 2 x = 0

E 1 y =   + E 1 sin ⁡ θ     &   E 2 y = + E 2 sin ⁡ θ  

E y = E 1 y + E 2 y = 262,8 ⋅ 0,8 + 262,8 ⋅ 0,8 ≅ 1380   N / C

Assim:

E = E x + E y = 0 + 1380 = 1380 N / C ,       n a   d i r e ç ã o   + y

Resposta

( a )

E = 0

E x = 0

E y = 0

( b )

E = 2663,1   N / C   n a   d i r e ç ã o   d e + x

E x =   2663,1   N / C

E y = 0   N / C

( c )

E = 526   N / C ,   a n t i - h o r a r i o     e m   284 ° d e + x ,     p a r a   b a i x o  

E x = + 129,4   N / C

  E y = - 509,7   N / C

d

E = 1380   N / C ,       n a   d i r e ç ã o   + y  

  E x = 0  

E y = 1380   N / C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas cargas puntiformes de módulos Q 1 = 2,0 ∙ 10 - 7 CeQ 2 = 8,5 ∙ 10 - 8 C estão separadas por uma distância de 12cm. (a) Qual o módulo do campo elétrico que cada uma cria no local onde está a outra
Um elétron está localizado em cada um dos vértices de um triangulo equilátero, que tem 20cm de lado. (a) Qual o campo elétrico no ponto médio de um dos lados? (b) Que força atuaria sobre um outro elét
Duas cargas iguais, mas de sinais opostos de módulo 2,0 ∙ 10 - 7C são mantidas a uma distância de 15cm uma da outra. (a) Quais são o módulo, a direção e o sentido de E no ponto situado a meia distânci
(a) Na Fig. 24-27, localize o ponto (ou os pontos) onde o campo elétrico resultante é nulo. (b) Esboce, qualitativamente, as linhas do campo elétrico.
Na Fig. 24-26, duas cargas puntiformes, q 1 = + 1,0 ∙ 10 - 6 Ceq 2 = + 3,0 ∙ 10 - 6 C , estão separadas por uma distância d=10cm. Faça o gráfico do campo elétrico resultante E(x) em função de x, toman