Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 22
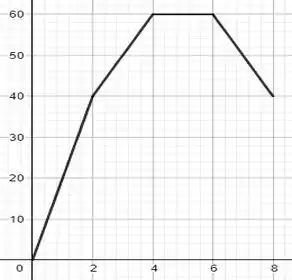
22. A FIGURA EX4.22 mostra o gráfico velocidade angular versus tempo para uma partícula movendo-se em um círculo, partindo de em . Desenhe o gráfico posição angular versus tempo. Inclua escalas adequadas em cada eixo.
Passo 1
Para fazer o gráfico que é pedido no enunciado primeiro vamos analisar o comportamento da partícula a parti do gráfico que temos, pois assim podemos encontrar o deslocamento angular, já que:
A partir disso podemos saber quanto a partícula se deslocou em um intervalo de tempo.
Passo 2
Vamos começar análise do gráfico então.
Temos que de até temos uma velocidade angular de , assim temos que .
De até temos uma velocidade angular de , assim temos que .
De até temos uma velocidade angular de , assim temos que .
E por último temos que de até temos uma velocidade angular de , assim temos que .
Passo 3
A partir da análise do passo anterior temos o seguinte gráfico do deslocamento angular em função do tempo:
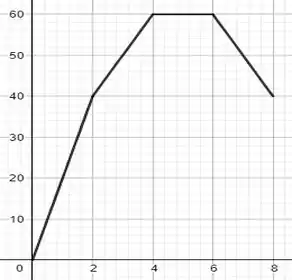
Resposta
