Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 59
Durante uma competição de aeromodelismo controlado por rádio, cada avião deve voar do centro de um círculo de 1,0 km de raio para qualquer ponto do círculo, e retornar ao centro. O vencedor é o avião com o menor tempo de ida-e-volta. Os concorrentes são livres para fazer seus aviões voarem seguindo qualquer rota, desde que o avião comece no centro, viaje até o círculo, e depois retorne ao centro. No dia da prova, um vento constante sopra do norte a 5,0 m/s. Seu avião pode manter uma rapidez no ar parado de 15 m/s. Você deve fazer seu avião voar contra o vento na ida e a favor do vento na volta, ou cruzando o vento coando primeiro para leste e depois para o oeste? Aumente suas chances calculando o tempo de ida-evolta para ambas as rotas, usando seus conhecimentos sobre vetores e velocidades relativas. Com este cálculo prévio, você pode decidir pela melhor rota e levar vantagem na competição!
Passo 1
MEU DEUS, QUE TEXTÃO!!!
Relaxa e vem comigo entender o que o problema ta dizendo !
O avião tem que sair do centro do circulo e ir para a borda do circulo e depois voltar ao centro! E ele tem que fazer isso no menor tempo possível.
Se é no menor tempo, imaginamos que sua rota vai ser uma reta, porque se ele ficar dando voltas e piruetas o tempo vai ser maior e não é isso que a gente quer.
Então o que temos aqui!?
Independentemente para que ponto da borda o avião for, a distância percorrida na ida, e depois na volta, vai ser igual a do raio do círculo!
Ai entra outra questão, tem o vento que sopra em velocidade constante do norte para o sul e a velocidade do avião com o ar parado é .
E o problema sugere duas rotas diferentes. A gente tem que calcular o tempo de voo nos dois casos e ver qual caso dá um tempo de vôo menor pra gente ganhar a corrida.
Ele já dá a dica para gente usar os conhecimentos de velocidade relativa. Então a gente precisa relacionar as velocidades do problema por uma soma vetorial:
Ou seja, a velocidade do avião em relação ao chão é igual a soma da velocidade do avião em relação ao ar com a velocidade do ar em relação ao chão (velocidade do vento).
A parada é usar essa soma para cada situação. Então vamos nessa!!!
Passo 2
Na primeira rota o avião vai voar primeiro contra ao vento e na volta ele vai voar a favor. Vamos fazer um desenho pra entendermos melhor!
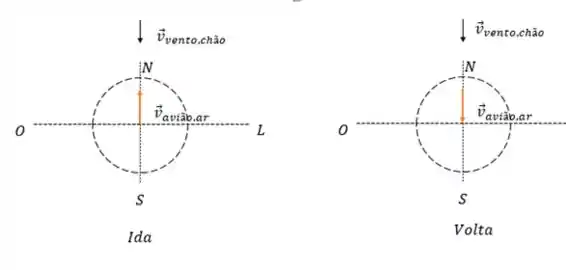
Vamos calcular a velocidade do avião em relação ao chão nos dois casos para depois descobrir o tempo, já que a velocidade em relação ao chão vai ditar nossa trajetória e deslocamento.
Na ida o avião esta indo contra o vento, logo nossa soma vai ser uma relação entre as componentes verticais dessas velocidades (já que todas estão na vertical):
Na volta ele esta indo a favor, então temos
Passo 3
Mas o que a gente quer é o tempo! A velocidade é
Isolando :
O tempo de ida fica:
E o de volta:
Lembrando que o raio é , como a velocidade esta em devemos escrever o raio em metros, com isso
Queremos o total, então temos que somar o tempo de ida com o tempo de volta:
Passo 4
Agora vamos calcular o para a segunta rota. Nesse caso o avião vai na direção leste e depois volta na direção oeste, dessa forma aqui:
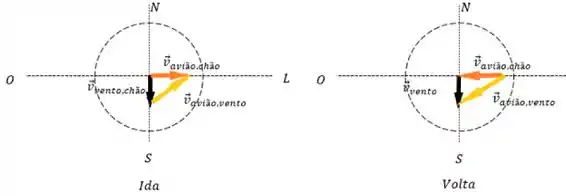
Nesse caso, como o avião (vetor laranja) atravessa o vento (vetor preto) perpendicularmente, a velocidade do avião em relação ao chão na ida e de volta vão ser numéricamente iguais.
E para calcular ela fazemos vamos usar o teorema de pitágoras:
Isolando :
Substituindo:
Agora podemos calcular o , lembrando que a distância é o dobro do raio agora porque essa é a velocidade de ida e volta:
Se para a primeira rota , maior do que , então a segunda rota é a melhor!
Resposta
Comparando os dois resultados, é possível notar que o tempo do trajeto cruzando o vento é menor, portanto seria o mais interessante a ser feito.