Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.1 - Ex. 5b
2.5b Dois corredores partem simultaneamente do mesmo ponto de uma pista circular de 200 m e correm em direções opostas. Um corre a uma velocidade constante de 6,20 m/s e o outro corre a uma velocidade constante de 5,50 m/s. Quando eles se cruzam pela primeira vez, b) Qual a distância percorrida por cada um deles?
Passo 1
Vamos lá!! Aqui temos duas pessoas que começam a correr a partir do mesmo ponto mas em direções opostas em uma pista circular de . Assim:
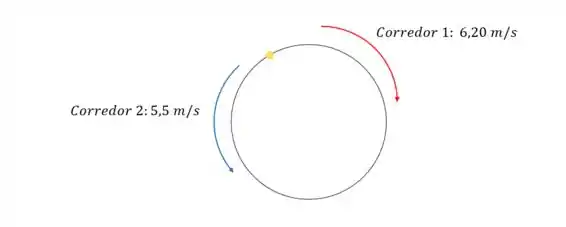
Queremos saber qual é a distância que cada corredor percorre antes de se encontrarem pela primeira vez!
Lá na letra (a) vimos que pra um mesmo tempo o corredor vai percorrer uma distância maior que o corredor por conta da sua velocidade maior. Além disso a soma das duas distâncias tem que ser igual a , então:
Também calculamos em que tempo vai acontecer esse encontro:
Passo 2
Temos a faca e o queijo na mão! É só multiplicarmos o tempo pela velocidade de cada corredor. Começando pelo primeiro:
Agora o segundo corredor:
Também poderíamos ter feito:
Dá uma diferencinha por causa dos arredondamentos!
Resposta
106 metros e 94,1 metros.