Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 26
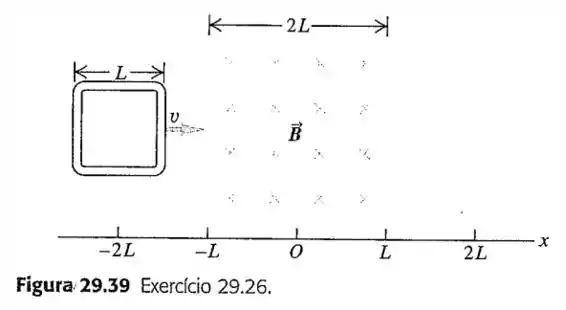
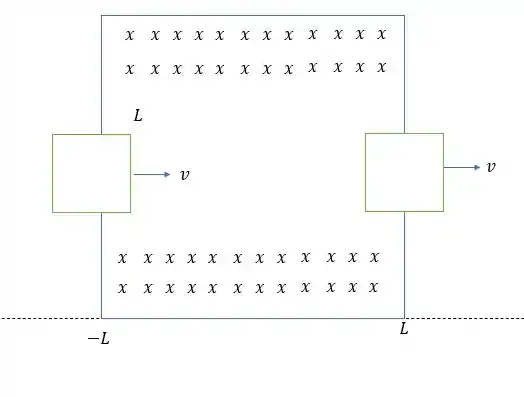
26- Uma espira quadrada, com resistência , se move com velocidade constante através de um campo magnético uniforme que está confinado em uma região delimitada por um quadrado de lado igual ao dobro do lado da espira quadrada (Figura )
Faça um gráfico da força externa necessária para fazer a espira se deslocar com velocidade constante em função da coordenada desde até . (A coordenada é medida do centro da região onde existe o campo magnético até o centro da espira quadrada. Ela é negativa enquanto o centro da espira está do lado esquerdo do centro da região onde existe o campo magnético. Considere positivo o sentido da força orientada para a direita)
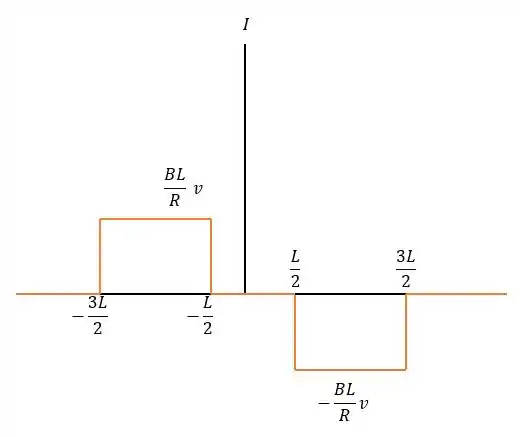
Faça um gráfico da corrente induzida na espira em função da coordenada .Considere positivo o sentido anti-horário da corrente.
Passo 1
Existem três regiões muito simples de se calcular o campo magnético você sabe? Pois é, quando a espira está totalmente fora da região com campo magnético, e essa região totalmente fora do campo magnético é quando e , pois é quando (que é o centro da espira) está meio para fora desse campo ou seja:
E como não há nenhum campo magnético na espira então a corrente que passa sobre ela é zero (não havendo fluxo magnético), e portanto não há força magnética, logo não haverá força externa.
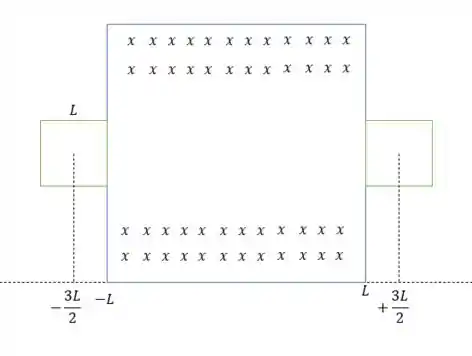
E outra região muito simples é quando a espira está totalmente dentro da espira, pois aí não haverá nenhuma variação do campo magnético aplicado sobre ela, ou seja:
E como não há variação da força magnética na espira na região entre , então não há variação de fluxo magnético (até tem fluxo magnético nela que vale porém não há variação) e portanto e ocasionando em , então a força externa para manter a velocidade constante é zero.
Passo 2
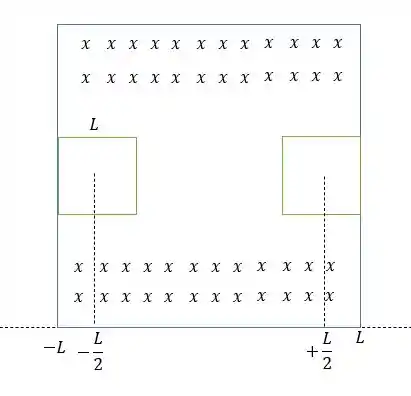
A brincadeira começa quando a espira está entrando e saindo do campo magnético.
Ou seja no intervalo de e e nesse intervalo sempre terá uma barra vertical da espira com um potencial elétrico maior que o outro (um nulo e outro igual a ) isso sabendo-se que as barras horizontais dessa espira não geram tensão elétrica, pois a barra deve estar perpendicular com a velocidade, logo a fem total da espira será:
Nos dando uma corrente induzida igual a:
Então a força magnética será de:
E como não há nenhuma aceleração na espira então a força externa deverá ser igual a a essa força magnética. E esse é o módulo nas duas regiões, agora e o sentido?
Passo 3
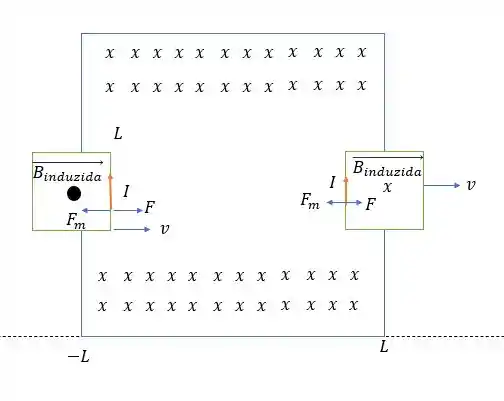
Quando a bobina está entrando na região o campo magnético induzido tende a sair do centro da espira (pois a componente entrando está aumentando) isso faz surgir uma componente de corrente no sentido anti-horário, portanto pela regra da mão esquerda a força magnética na barra a direita (dentro do campo e que gera a fem) aponta para a esquerda , para anular a força externa deverá estar para a direita.
Já quando a bobina está saindo o campo magnético entrando no centro da bobina está diminuindo portanto o campo magnético induzido está entrando no centro da bobina também, isso faz criar uma corrente no sentido horário, isso faz com que a força magnética na barra a esquerda esteja apontada para a esquerda, então para compensar a força externa severa estar para a direita.
Isso tudo que disse tá representada na figura abaixo.
Passo 4
Dessa forma os gráficos de e de serão:
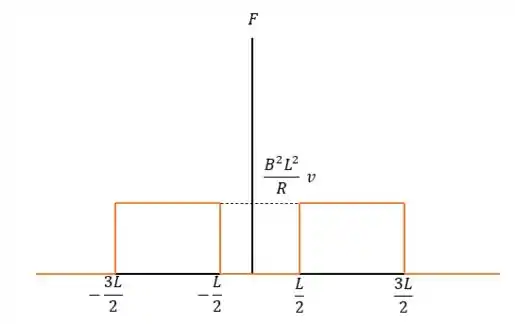
E a corrente:
