Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 28

28- Um solenoide fino possui 900 espiras por metro e raio igual a 2.50   c m . A corrente no solenoide cresce com uma taxa uniforme de 60.0   A / s . Qual é o módulo do campo elétrico induzido em um ponto próximo do centro do solenoide e situado a uma distância do eixo do solenoide.

( a ) igual a 0.500   c m ?

( b ) igual a 1.0   c m ?

Passo 1

O módulo do campo elétrico induzido é encontrado pela Lei de Faraday:

∮ E → ⋅ d l → = d ϕ B d t = d B d t A

Onda a superfície distante de uma distância r é igual ao círculo de raio r , então:

E ⋅ 2 π r = d B d t   π r 2

Pois a área é a área do círculo de raio r que especificamos.

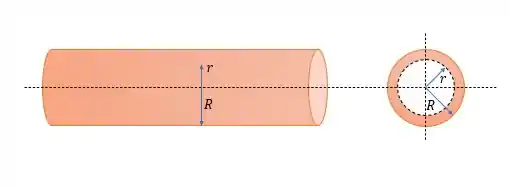
Pois temos que considerar esse r dentro do ‘’cilindro’’ do solenoide (isso que significa estar próximo do centro do solenóide).

Então o módulo do campo elétrico será igual a:

E = d B d t r 2

Agora precisamos lembrar que o campo magnético de uma solenoide é dada por:

B = N L μ 0 I

E como N / L é fixo e vale 900 , μ 0   é uma constante de I é a única coisa que variará então:

d B d t = N L μ 0 d I d t

Então:

E = N L μ 0 d I d t r 2  

Passo 2

Então para r = 0.5 × 10 - 2 teremos:

E = 900 × 4 π × 10 - 7 × 0.5 × 10 - 2 2 × 60 = 1.7 × 10 - 4   V / m

E para r = 10 - 2   c m

E = 900 × 4 π × 10 - 7 × 10 - 2 2 × 60 = 3.39 × 10 - 4   V / m

Resposta

a )   E = 1.7 × 10 - 4   V / m

b )   E = 3.39 × 10 - 4   V / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a auto-indutância equivalente para dois indutores que têm auto-indutâncias L 1 e L 2 e estão conectados em série é dada por L e q = L 1 + L 2 se não há acoplamento de fluxo entre os dois in
Mostre que a auto-indutância equivalente para dois indutores que têm auto-indutâncias L 1 e L 2 e estão conectados em paralelo é dada por 1 L e q= 1 L 1 + 1 L 2 se não há acoplamento de fluxo entre os
Uma barra longa cilíndrica, de material cuja suscetibilidade magnética é χ m ≪ 1 , transporta uma corrente elétrica com densidade uniforme j → = jz ^ . Calcule: (a) a magnetização da barra em função d
Calcule a intensidade do campo H à distância de 10c m de um fio longo transportando uma corrente de 30A .
Considere as medidas de força magnética ilustradas na Figura 25.1 do texto. Supondo que M ≪ H , mostre que a suscetibilidade magnética da partícula pode ser expressa por χ m = ρ g μ 0 B x ∂ B x ∂ x ⋅