Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 9.Problemas - Ex. 9
Uma pequena espira circular de raio percorrida por uma corrente desliza com velocidade constante ao longo do eixo de outra espira de raio e resistência , aproximando-se dela, com os planos das duas espirar paralelos. Calcule a corrente induzida na espira de raio para uma distância entre os centros das duas espiras. Qual é o sentido relativo das correntes nas duas espiras?
Passo 1
Vamos primeiro tomar visualmente o que foi nos apresentado
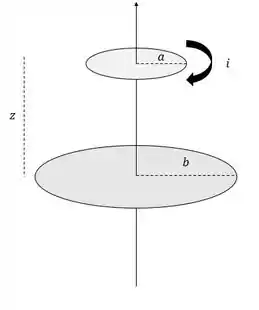
Ou seja, temos duas espiras, na qual a menor, de raio , desce com uma velocidade .
O enunciado nos da que a espira de raio tem uma corrente igual a . Sabemos que quando uma corrente percorre um fio, ela gera na direção radial, um campo magnético .
Em uma espira temos que o campo magnético gerado a uma distância do centro da espira é dado por
Não acredita? Nos provamos https://bit.ly/3bTJHyd . Responde ai não mente hahaha...
Passo 2
Então sabemos do passo 1 que o campo que a espira de raio gera é de
A primeira condição de contorno é que , assim temos que
Implicando que teremos que nosso campo será nesta condição
Passo 3
Quando a espira vê a espira se aproximando, ela sente o campo magnético gerado pela espira . Quanto mais a espira se aproxima, temos que o fluxo em varia. Dizemos que a corrente induzida em é dada por
Na qual a força eletromotriz induzida é dada por
Fluxo esse que é gerado pela espira . O fluxo é dado por
Ou seja, o fluxo que passa pela área da espira é gerado pela espira como dissemos e estamos reforçando vezes a área da espira .
Assim temos então que
Assim teremos que a variação do fluxo com o tempo será
Ou seja
Pela lei de Lenz, temos que o sentido da corrente é oposta a da espira que gera o campo indutor.