Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.1 - Ex. 6
2.6 Suponha que os dois corredores do Exercício 2.5 partem ao mesmo tempo, do mesmo ponto, mas correm na mesma direção. a) Quando o mais rápido ultrapassará o mais lento e a que distância do ponto de largada cada um estará? b) Quando o mais rápido ultrapassará o mais lento pela segunda vez e, nesse instante, a que distância cada um estará do ponto de largada?
Passo 1
Vamos lá! Aqui a gente vai usar os mesmos corredores do exercício . Eles saem do mesmo ponto em direções opostas. Da seguinte forma:
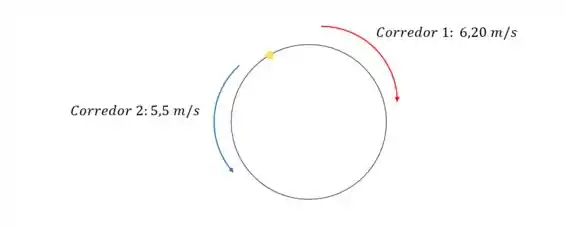
Essa pista tem e queremos saber, na letra (A) em que tempo os corredores vão se cruzar pela segunda vez e a que distância do ponto de largada cada um estará.
Como o mais rápido é mais rápido (obviedades, a gente ver por aqui!), ele já sai na frente. Como a pista é circular, ele só vai ultrapassar o mais lento, ou seja, encontra-lo pela segunda vez, quando der uma volta a mais na pista (de 200m) do que o mais lento.
Então temos que o deslocamento do mais rápido é igual ao deslocamento do mais lento mais esses outros 200 metros da volta.
“E como achar essa posição?”
Vem comigo!
Passo 2
Aqui a questão nos pede o tempo de ultrapassagem e a distância percorrida por cada um nesse momento. Vamos achar primeiro o tempo usando o nosso delicioso “sorvete”:
Mas a gente tem a velocidade e o , que é 0. Então dá pra dar uma arrumadinha e ficarmos com só duas variáveis.
Passo 3
Como a distância percorrida pelo mais rápido é a distância do mais lento com mais 200 metros da volta, temos:
E achamos o tempo!
Passo 4
Agora só falta multiplicar esse tempo pela velocidade dos dois usando a fórmula do passo 2:
E achamos a distância dos dois! \o/
Bora pra letra b!
Passo 5
Se na primeira volta ele teve que andar 200 metros a mais pra ultrapassar, na segunda volta ele vai ter que andar mais 200, ou seja, 400 metros a mais. O resto é tudo igual, então vem com a gente!
O deslocamento do mais rápido é igual ao do mais lento mais 400 metros, então temos:
Temos aí o tempo.
Passo 6
Agora é só multiplicar esse tempo pelas velocidades:
Achamos as distâncias e terminamos a questão, pimpolhos! \o/
Resposta
- 286 segundos; 1770 metros, 1570 metros
- 572 segundos; 3540 metros, 3140 metros