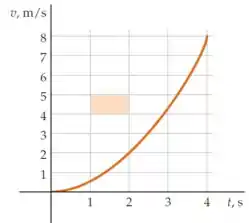
A figura abaixo mostra a velocidade de uma partícula em função do tempo; (a) Qual é a magnitude, em metros, representada pela área do retângulo sombreado? (b) Estime o deslocamento de uma partícula para os dois intervalos de 1-s, um começando em e o outro em . (c) Estime a velocidade média para o intervalo . (d) A equação da curva é . Encontre o deslocamento da partícula para o intervalo por integração e compare essa resposta com a do item (b); A velocidade média é igual à média das velocidades final e inicial nesse caso?

(b) Como podemos encontrar o deslocamento a partir de um gráfico de velocidade em função do tempo? É só calcular a área sob o gráfico.

Mas como o enunciado pediu apenas uma “estimativa”, nós podemos simplesmente “contar os quadrados” sob o gráfico nos dois intervalos.

Entre e , podemos contar “mais ou menos” um quadrado e inteiro e mais de um quadrado:

E entre e , podemos contar mais ou menos três quadrados inteiros e mais de outro:

(c) Para calcular a velocidade média no intervalo de até o , nós precisamos usar a seguinte fórmula:

E pela conta que acabamos de fazer, o deslocamento total é aproximadamente:

E isso tudo acontece em um intervalo de tempo , então:

(d) Agora vamos integrar a função da velocidade em relação ao tempo para encontrar o deslocamento no intervalo .

Que é um resultante bastante próximo do encontrado no item (), considerando que o método que usamos nesse caso foi o de “contar quadrados”.

Por último queremos saber se, no caso desse intervalo , a velocidade média é igual à média das velocidades final e inicial.

Nós calculamos a velocidade média desse intervalo no item (c), e encontramos o seguinte:

Agora vamos comparar isso com a média das velocidades final e inicial que nós podemos calcular com a função que foi dada no enunciado:

E então:

Que é um valor diferente! Isso é de se esperar, considerando que no caso do enunciado não temos aceleração constante.