Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 31
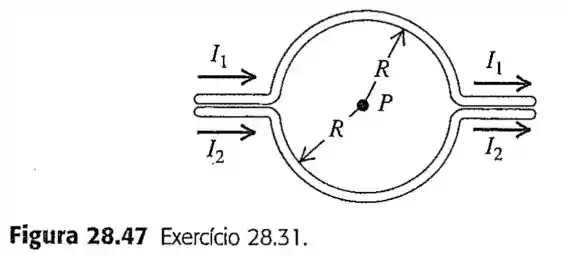
31- Calcule o módulo do campo magnético resultante produzido no ponto da Figura em função de e . O que sua expressão fornece quando ?
Passo 1
Nas seções retas, não temos nenhuma influência magnética em pois a corrente e o ponto se situam na mesma horizontal ou seja:
E o vetor direção do campo magnético:
Isso independente do sentido da corrente, portanto todas as quatro partes horizontais da seção não produzirão nenhum campo magnético resultante.
Passo 2
Agora para as espiras circulares, mais precisamente a superior, por ser semicircular nela você terá um campo magnético de módulo igual a:
Com o sentido do campo magnético (pela regra da mão direita), entrando no sentido da folha (sentido negativo de ).
E na espira de baixo você terá o surgimento de um campo magnético igual a:
Como sentido a sair da folha do papel (sentido positivo de ) então somando-se os sentidos temos que o campo total será igual a:
Como então o campo magnético total em será nulo.