65- Uma espira circular de raio a possui N espiras e conduz uma corrente I . Uma segunda espira circular de raio a ' possui N ' espiras e conduz uma corrente I ' e seu centro está localizado sobre o eixo da primeira espira, a uma distância x do centro da primeira espira. A segunda espira é inclinada, de modo que seu eixo forme um ângulo θ com o eixo da primeira. A distância x é maior do que a e a ' . ( a ) Determine o torque que a primeira exerce sobre a segunda. ( b ) Calcule a energia potencial para a segunda espira em virtude dessa interação. ( c ) Qual é a simplificação que obtemos considerando x muito maior do que a ? E para x muito maior do que a ' ?

a )τ = μ 0 N N ' I I ' a 2 π a 2 ' 2 x 3 sin ⁡ θ b )U = - μ 0 N N ' I I ' a 2 π a 2 ' 2 x 3 cos ⁡ θ c )p a s s o3

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 65

65- Uma espira circular de raio possui espiras e conduz uma corrente . Uma segunda espira circular de raio possui espiras e conduz uma corrente e seu centro está localizado sobre o eixo da primeira espira, a uma distância do centro da primeira espira. A segunda espira é inclinada, de modo que seu eixo forme um ângulo com o eixo da primeira. A distância é maior do que e .

Determine o torque que a primeira exerce sobre a segunda.

Calcule a energia potencial para a segunda espira em virtude dessa interação.

Qual é a simplificação que obtemos considerando muito maior do que ? E para muito maior do que ?

Passo 1

Não sei se vai ajudar por que arranjei umas espiras feias a beça mas o que está sendo retratado no enunciado é a figura abaixo.

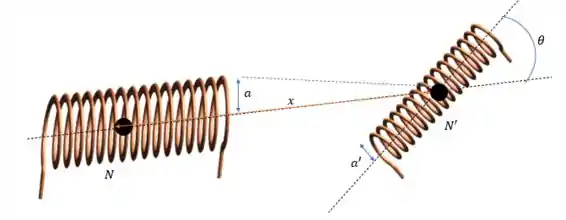
Onde e

Então o campo magnético que a primeira espira circular gera na segunda espira será de:

Mas como então a influência da primeira bobina na segunda será de:

Onde o torque acontece com a direção área da seção transversal da segunda bobina e que tem que estar perpendicular o campo magnético, como o campo magnético é produzido no mesmo eixo da primeira espira, então para que a área da segunda fique perpendicular a ela nós devemos colocar o termo e são características da segunda espira. Portanto:

Aqui também devemos assumir que pois aí podemos assumir que o campo magnético da primeira bobina é constante para todo o comprimento da segunda bobina.

Passo 2

Já a energia é dada por:

Qualquer dúvida revise o capítulo 27.

Passo 3

Fazendo foi possível simplificar a fórmula do campo magnético no centro da segunda espira e fazendo foi possível assumir que o campo magnético gerado pela primeira bobina era constante por toda a segunda bobina.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

75- A espira retangular indicada na Figura 27.65 possui massa igual a 0.15g por centímetro de comprimento e está articulada em torno do lado a b por meio de um eixo sem atrito. A corrente que circula

85- Uma espira circular de área A está contida no plano x y . Vista ao longo do eixo O z , olhando para a origem no sentido - z , uma corrente I circula no sentido horário em torno da espira. O torque

84-Derivação da Equação (27.26) para uma espira circular. Uma espira em fio em forma de anel está sobre o plano x y com o centro na origem. No anel, circula uma corrente I no sentido anti-horário (Fig

82- Torque sobre uma espira de corrente em um campo magnético não uniforme. Na Seção 27.7 , a expressão do torque sobre uma espira de corrente foi deduzida supondo que o campo magnético B → fosse unif

31- Calcule o módulo do campo magnético resultante produzido no ponto P da Figura 28.47 em função de R , I 1 e I 2 . O que sua expressão fornece quando I 1 = I 2 ?