Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 50

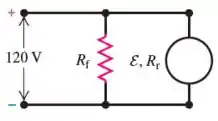
A figura 27.56 mostra uma fonte de alimentação de 120   V ligada a um motor cc com shunt, no qual o rotor está ligado em paralelo às bobinas de campo. A resistência das bobinas de campo é R f = 218   Ω . A resistência do rotor é R r = 5,9   Ω . Quando o motor está funcionando, o rotor desenvolve uma f e m   ε . O motor consome uma corrente igual a 4,82   A da fonte. As perdas por atrito correspondem a 45,0   W . Calcule: (a) a corrente que passa nas bobinas de campo; (b) a corrente no rotor; (c) a f e m   ε ; (d) a taxa de produção de energia térmica no rotor; (f) a potência fornecida ao motor; (g) a eficiência do motor.

Passo 1

letra a)

A bobina e o rotor estão em paralelo, logo possuem o mesmo potencial. Então:

i f = V R f

i f = 120 218

i f = 0,55   A

Passo 2

letra b)

Sabemos a corrente fornecida ao motor e a corrente na bobina. Logo:

I = i f + i r

i r = I - i f

i r = 4,82 - 0,55

i r = 4,27   A

Passo 3

letra c)

A fem induzida desenvolvida pelo motor é dada por:

ε = V - i r R r

ε = 120 - 4,27 ⋅ 5,9

ε = 94,8   V

Passo 4

letra d)

A taxa de produção de energia térmica no rotor é dada pela potência dissipada no mesmo.

P = i r 2 R r

P = 4,27 2 ⋅ 5,9

P = 108   W

Passo 5

letra f)

A potência fornecida ao motor será:

P = V I

P = 120 ⋅ 4,82

P = 578   W

Passo 6

letra g)

A eficácia é dada pela razão entre a potência que sai e a potência que entra no motor.

Ou seja, a potência que sai é a potência do fornecida menos as potências dissipadas.

η = P s a i P e n t r a

η = 578 - P r + P f + P a t r i t o 578

η = 578 - 108 + 0,55 2 ⋅ 218 + 45 578

η = 0,621

Resposta

letra a) i f = 0,55   A

letra b) i r = 4,27   A

letra c) ε = 94,8   V

letra d) P = 108   W

letra f) P = 578   W

letra g) η = 0,621

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas espiras, uma em forma de circunferência e outra em forma de quadrado, têm o mesmo comprimento L e conduzem a mesma corrente i . Mostre que o campo magnético produzido no centro da espira quadrada
A Eq. 29-4 fornece o módulo B do campo magnético criado por um fio retilíneo infinitamente longo em um ponto P situado a uma distância R do fio. Suponha que o ponto P esteja, na verdade, a uma distânc
Na Fig. 29-43, o ponto P 1 está a uma distância R = 13,1c m do ponto médio de um fio retilíneo de comprimento L = 18,0c m que conduz uma corrente i = 58,2m A . (Observe que o fio não é longo.) Qual é
Calcular o campo magnético B no ponto P da Fig. 31-41. Suponha que i = 10 A e a= 8.0 cm.
A Fig. 31-42 mostra uma seção transversal de uma fila comprida e fina, de largura w, que está transportando uma corrente i uniformemente te distribuída, para o interior da página. Calcular o módulo, a