Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 32.Exercício - Ex. 35
35- Forno de micro-ondas. As micro-ondas de um forno de micro-ondas possuem um comprimento de onda de
Qual deve ser a largura desse forno para que possa conter cinco planos antinodais do campo elétrico ao longo da sua largura no padrão de onda estacionário?
Qual é a frequência dessas micro-ondas?
Suponha que, por um erro de fabricação, o forno tenha ficado mais comprido do que o item especificado no item . Nesse caso, qual teria de ser a frequência das micro-ondas para ainda haver cinco planos antimodais do campo elétrico ao longo da largura do forno?
Passo 1
O comprimento de onda que cabe planos antinodais (pontos com bolinha fechada) é o comprimento que cabe planos nodais, uma vez que o campo elétrico para uma onda estacionária é uma onda senoidal e não contamos os pontos que ficam junto com os planos.
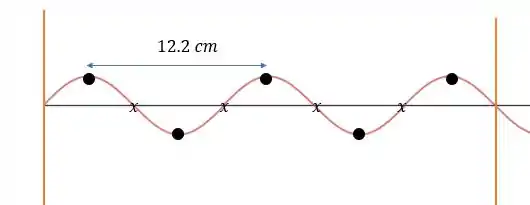
Então teremos 2 comprimentos de onda mais uma metade para caber nesse micro-ondas aí.
Passo 2
Por nós conseguiremos encontrar a frequência da onda, pois por mais que o micro-ondas possa ser sujo as vezes isso não interfere na velocidade da onda , então assim sendo:
Passo 3
Aumentando a parede do micro-ondas e mantendo a característica do campo elétrico ter cinco-antinodais nós teremos um novo comprimento de onda igual a:
O que nos dá uma frequência de:
O que diminui um pouco a frequência das ondas. E é por conta dessa alta frequência (que é bem perigosa se você estiver em frente a um magnétron não protegido inclusive) que os micro-ondas tem um tamanho bem razoável até.