Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 32.Problemas - Ex. 53

53- Sistema de Posicionamento Global (GPS). A rede G P S consiste de 24 satélites, e cada qual realiza duas órbitas em torno da Terra por dia. Cada satélite transmite um sinal eletromagnético senoidal de 50.0   W (ou até menos) em duas frequências, uma das quais é de 1575.42   M H z . Suponha que um satélite transmita metade da sua potência em cada frequência e que as ondas se propaguem uniformemente em um hemisfério de cima para baixo.

( a ) Qual é a intensidade média que um receptor de G P S no solo, diretamente abaixo do satélite, recebe? (Sugestão: primeiro use as leis de Newton para determinar a altitude do satélite.)

( b ) Quais são as amplitudes dos campos elétrico e magnético do receptor de G P S no item ( a ) , e quanto tempo leva para o sinal atingir o receptor?

( c ) Se o receptor for um painel quadrado de 1.50   c m de lado que absorve todo o feixe de luz, qual é a pressão média exercida pelo sinal sobre ele?

( d ) Qual é o comprimento de onda com o qual o receptor deve estar sintonizado?

Passo 1

Para um satélite estar em órbita então temos que a força gravitacional que atrai o satélite para a Terra

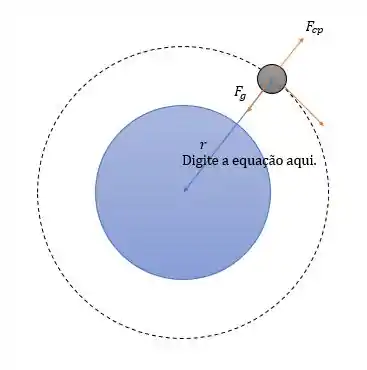
Então igualando as duas forças teremos:

F g = F c p

G M m r 2 = m v 2 r

Onde a velocidade desse satélite será:

v = 2 π r T

Que é a distância do perímetro de revolução sobre o tempo de revolução. Então r será:

G M m r 2 = m 4 π 2 r 2 T 2 r

r 3 = G M T 2 4 π 2

r = G M T 2 4 π 2 1 3

Onde a massa da Terra será pelo apêndice F na edição 5 será M = 5.97 × 10 24   k g 3 G = 6.67 × 10 - 11 N m 2 k g 2

Então:

r = 6.67 × 10 - 11 × 5.97 × 10 24 × 12 × 3600 2 4 π 2 1 3 = 2.66 × 10 7   m

Pois como o satélite realiza duas órbitas em torno da terra por dia então o período do satélite é de 12   h o r a s e teremos que converter para segundos.

Passo 2

Só que essa distância r é a distância do satélite até o centro da Terra, e como vivemos na superfície da Terra então temos que a altitude h será:

r = h + r T E R R A

Onde o raio da Terra será 6.38 × 10 6   m pelo apêndice F .

h = 2.66 × 10 7 - 6.38 × 10 6 = 2.022 × 10 7   m

Então a intensidade média da onda eletromagnética será:

I = P 4 π h 2 = 25 2 π 2.022 × 10 7 2 = 9.732 × 10 - 15 W m 2

Pois é transmitido metade da potência na metade da área da esfera.

Passo 3

Então encontrando a amplitude do campo elétrico na letra b será:

I = 9.732 × 10 - 15 = E m á x 2 2 μ 0 c → E m á x = 2.71 × 10 - 6 V m

Então a amplitude do campo magnético será:

B m á x = E m á x c = 2.71 × 10 - 6 3 × 10 8 = 9.03 × 10 - 15 T

Como a velocidade de propagação da onda é uma velocidade constante c e ele percorre uma distância h então o tempo de propagação será de:

c = h t → t = h c = 2.022 × 10 7 3 × 10 8 = 0.0674   s

Passo 4

Como na letra c a superfície é totalmente absorvedora então a pressão exercida sobre ele será:

p = I c = 2 × 9.732 × 10 - 15 3 × 10 8 = 3.244 × 10 - 23   P a

Passo 5

E para fechar o comprimento de onda será:

c = λ f

Onde a frequência dada é de 1575.42 × 10 6   H z , então:

λ = 3 × 10 8 1575.42 × 10 6 = 0.19   m

Resposta

a )   I = 9.732 × 10 - 15 W m 2

b ) E m á x = 2.71 × 10 - 6 V m ; B m á x = 9.03 × 10 - 15 T ; t = 0.0674   s

c ) p = 3.244 × 10 - 23   P a

d )   λ = 0.19   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o valor médio da componente vertical do campo magnético da Terra é 43μ T (para baixo) em todo o estado americano do Arizona, que tem uma área de 2,95 ⋅ 10 5k m 2 . Determine (a) o valor ab
Prove que a corrente de deslocamento em um capacitor de placas paralelas de capacitância C pode ser escrita na forma i d = C d V / d t , onde V é a diferença de potencial entre as placas .
Um capacitor de placas paralelas com placas circulares de 0.10m de raio está sendo descarregado. Um anel circular com 0,20m de raio, concêntrico com o capacitor, está a meio caminho entre as placas. A
Um capacitor de placas paralelas com placas circulares de raio R está sendo carregado. Mostre que o módulo da densidade de corrente da corrente de deslocamento é J d = ε 0 d E d t para r ≤ R .
Qual deve ser a taxa de variação da diferença de potencial entre as placas de um capacitor de placas paralelas com uma capacitância de 2 μF para que seja produzida uma corrente de deslocamento de 1,5