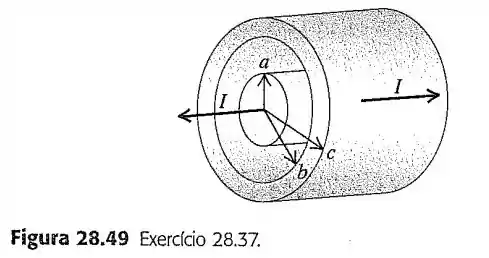
37- Cabo coaxial. Um condutor sólido com raio é suportado por discos isolantes no centro de um tubo condutor com raio interno e raio externo (Figura ). O condutor central e o tubo transportam correntes com o mesmo módulo , porém com sentidos contrários. As correntes são distribuídas uniformemente ao longo da seção reta de cada condutor. Deduza uma expressão para o módulo do campo magnético

nos pontos no exterior do condutor sólido central, porém no interior do tubo ();

nos pontos no exterior do tubo ()

Note da questão passada que a distância que cada corrente tem uma na outra não interfere na integral de linha da região.Então para a região de até nós temos:

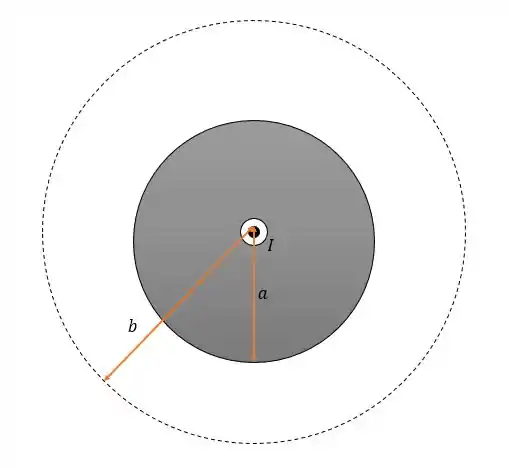
Dessa forma a integral de linha nessa região será:

Pois a corrente saindo gera uma integral de linha positiva, e como todas as regiões desse fio são círculos são círculos perfeitos então:

Pois o comprimento da linha é o comprimento de círculos de raio (qualquer) e independente de nesse caso. Então podemos dizer que:

Esse campo magnético é o campo que estará presente na região pois a lei de Ampere ela age em superfícies fechadas e cheias (não em regiões vazadas) então devemos englobar a região na análise.