Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 23
23- Quatro linhas de força longas e paralelas transportam correntes de . Um diagrama de seção reta dessas linhas é um quadrado, com de cada lado. Para cada um dos três casos indicados na Figura , calcule o campo magnético no centro do quadrado.
Passo 1
Primeira coisa que temos que ter noção aqui é como cada corrente mexe com o campo magnético no plano do papel e isso será feita da seguinte forma:
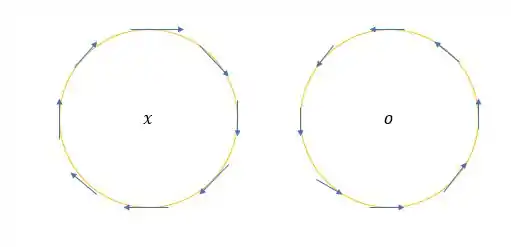
Então se tem um ponto de interesse está na diagonal da corrente o campo magnético terá um comportamento na diagonal de acordo com a imagem acima.
Passo 2
Então para a letra nós vamos ter:
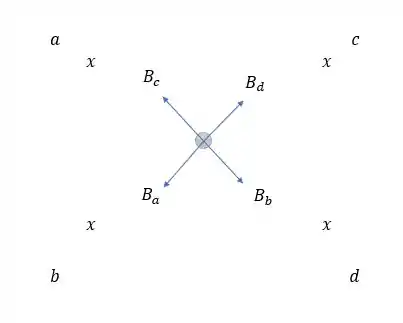
Então temos campo nulo, pois todos se anulam pois todos os vetores tem a mesma intensidade
Passo 3
Para a letra teremos:
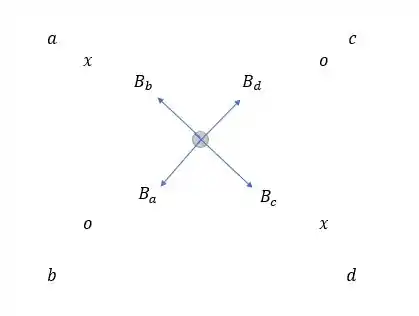
O que é a mesma coisa só invertemos o sentido de e de que são opostos.
Passo 4
Já para a letra :
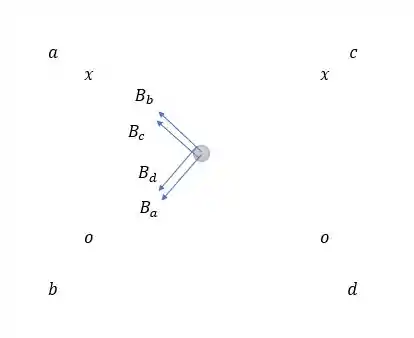
Vetor esse que apontará para a esquerda, pois se rebatermos o vetor na vertical o vetor se anulará com pois temos um quadrado, então os vetores estão angulados em . Dessa forma o vetor resultante será:
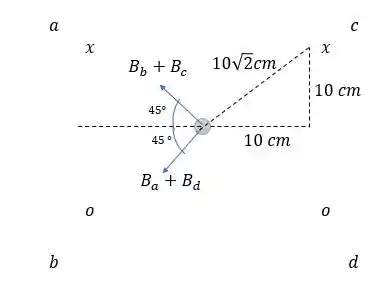
Sentido apontando para a esquerda.