Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 22.Exercícios e Problemas - Ex. 11
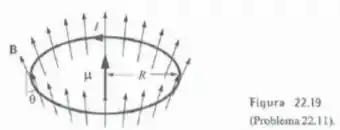
A figura 22.19 mostra um anel circular de raio transportando uma corrente , na presença de um campo magnético não uniforme. Em cada ponto do anel o campo tem a mesma intensidade e faz um ângulo com a normal ao plano daquele. Calcule a força que o campo faz sobre o anel.
Passo 1
Eai pessoal, beleza?
Antes de qualquer coisa, vamos definir um sistema de coordenadas. Para esse problema, é bem interessante usarmos coordenadas cilíndricas já que o anel tem esse tipo de simetria:
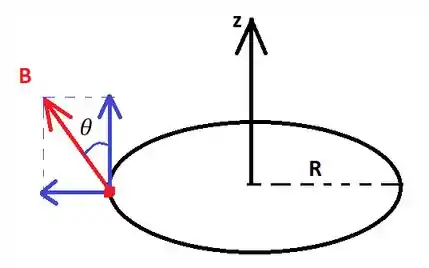
Na figura eu desenhei o vetor campo magnético sobre um elemento infinitesimal do anel. Em coordenadas cilíndricas com os versores , e , o campo magnético sobre o elemento pode ser escrito como
Uma das componentes do campo está na direção enquanto a outra está na direção radial. Vale ressaltar que todos os elementos do anel estão sobre ação do mesmo campo .
Podemos representar o elemento infinitesimal de fio vetorialmente por
É fácil perceber que esse elemento é tangencial ao fio.
Passo 2
A força infinitesimal que aparece no elemento é dada por
Logo,
Como e , temos que
Estamos quase terminando o problema, falta apenas integrar sobre todo o fio. Mas antes disso, observe que as componentes radiais da força em cada elemento vão se cancelar quando consideramos o fio todo, enquanto as componentes na direção se somam. Com isso, a força resultante será na direção :
A integral em será simplesmente o comprimento da circunferência , de modo que
Se quisermos apenas o módulo da força, temos