8- Um elétron e um protón se movem a cada um, em trajetórias perpendiculares, como indica a Figura . No instante em que eles estão nas posições indicadas na figura, determine o módulo, a direção e o sentido
do campo magnético total que eles produzem na origem
o campo magnético que o elétron produz na localização do próton
a força elétrica total e a força magnética total que o elétron exerce sobre o próton

Passo 1
Vamos por partes o vetor campo magnético na origem será calculado por:
Porém a posição dos dois em relação a oirgem será:
E a velocidade dos dois é de:
Então o campo magnético na origem será:
Não se esquecendo que a carga do próton é a mesma que a carga do elétron, só que a carga do elétron é negativa. Dessa forma:
Os dois campos magnéticos apontam para , ou seja para dentro da folha.
Passo 2
Como queremos o campo magnético que o elétron produz no próton então:
Então será:
Dessa forma:
Sentido entrando na folha .
Passo 3
A força elétrica exercida pelo elétron será de:
Força de atração, então:
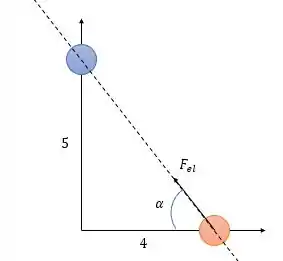
Passo 4
A força magnética do elétron no próton é devido ao campo magnético gerado por ele no ponto de interesse, portanto a força será: