Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 22.Exercícios e Problemas - Ex. 10
Calcule o campo magnético no ponto da Figura 22.18, o qual é o centro comum dos dois semicírculos.
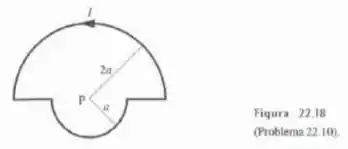
Passo 1
Eai pessoal, beleza?
Vamos nos preocupar primeiro com o campo produzido pelo semicírculo superior com raio :
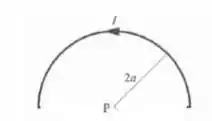
O campo produzido por um aro circular de raio e ângulo (em radianos) no centro da espira é dado por
Quando recuperamos o tradicional resultado da espira circular. Nesse caso, temos e , de modo que
Passo 2
Vamos considerar agora a porção de baixo:
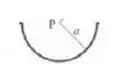
Temos e :
Esses dois campos apontam para fora da tela na sua direção! Somando os vetores:
Com isso, achamos
Resposta
Exercícios de Livros Relacionados
Na figura 29-70, um cano circular longo de raio externo R = 2,6c m conduz uma corrente (uniformemente distribuída) i = 8,00m A para dentro do papel. Existe um fio paralelo ao cano a uma distância de 3
A figura 29-67 mostra duas curvas fechadas que envolvem duas espiras que ocnduzem correntes i 1 = 5,0A e i 2 = 3,0A . Determine o valor da integral ∮ B → . d S → (a) para a curva 1 e (b) para a curva
A densidade de corrente J no interior de um fio cilíndrico longo de raio a = 3,1m m é paralela ao eixo central e o módulo varia linearmente com a distância radial r de acordo com a equação J = J o r /
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
A figura 29-79 mostra uma seção reta de um condutor cilíndrico longo de raio a = 4,00c m que contrém um furo cilíndrico de raio b = 1,50c m . Os eixos centrais do cilindro e do furo são paralelos e es