Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 46
46. Uma menina de massa está levando um lanche para o piquenique da avó. Ela amarra uma corda de comprimento , ao galho de uma árvore, sobre um riacho, e começa a se balançar, a partir do repouso, de um ponto que é mais baixo do que o galho. Qual a menor tensão de ruptura que a corda pode ter para não se romper atirando a menina no riacho ?
Passo 1
A primeira coisa a se fazer para resolver a questão é olhar a sua estrutura. Bem, o enunciado diz que há uma menina se balançando numa árvore em uma corda de comprimento e pede a menor tensão de ruptura para que a corda não se rompa. Isso cheira, a questão de pêndulo. E, se aprendemos bem, a primeira coisa que temos que fazer nesse tipo de exercício é representar a situação em uma imagem:
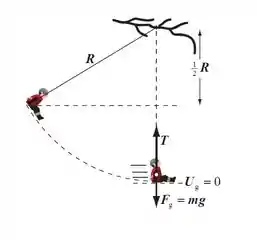
Que beleza! Agora as coisas vão começar a ficar mais claras.
O próximo passo, agora é definir qual será a nossa linha zero de energia potencial, a origem do nosso referencial. Como o que a gente quer é facilidade, vamos fazer o óbvio e escolher o ponto mais baixo de balanço como nossa origem.
Vamos aos cálculos:
Passo 2
Escolhido nosso referencial e entendido o que nosso problema quer, só nos resta agora, fazer o que é praxe em questões envolvendo pêndulos. Isso mesmo! Aplicar a Segunda Lei de Newton na direção radial, que diz que:
Temos, então da figura do que:
Só que esse é a velha e conhecida aceleração centrípeta:
Pronto, conseguimos a primeira equação. Agora, vamos prosseguir e dar início ao próximo passo
Passo 3
Adivinha o que vem aí? Isso mesmo, o princípio da conservação da energia mecânica. Uma vez que não tem forças externas atuando no nosso sistema, então a energia mecânica do ponto mais baixo é igualzinha a energia do ponto mais alto da trajetória da garota:
Só que .
Espera um pouco! Se e obtemos a seguinte relação, lá no :
Então:
Resposta
A menor tensão é