Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 49
49. Uma montanha-russa consiste em um único loop. O carrinho é, inicialmente empurrado, adquirindo a energia mecânica exatamente necessária para que os passageiros se sintam "sem peso" no ponto mais alto do arco circular. Eles se sentirão com qual peso ao passarem pela base do arco (ou seja, qual é a força normal exercida para cima quando eles estão na base do arco)? Dê sua resposta como um múltiplo de (o peso real dos passageiros). Desconsidere atrito ou resistência do ar.
Passo 1
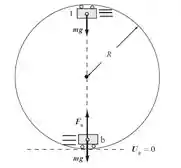
Sejam o raio do loop e a massa de um dos passageiros . No topo do circuito, a força centrípeta atuando sobre a pessoa é o seu peso (a força da gravidade). As duas forças que atuam sobre ela na parte inferior do circuito são a força normal exercida pelo banco do carro, empurrando-a para cima e a força da gravidade,puxando-a para baixo. O que temos que fazer, portanto, é aplicar a segunda lei de Newton, nas sitauções em que o carrinho encontra-se na base e no topo do arco circular. Aí sim! Mãos à obra!
Ahhh! Já ia esquecendo! O solo é a origem do nosso referencial gravitacial .
Passo 2
Vamos aplicar o somatório das forças na direção radial para os dois casos propostos no . Lembra aí que aceleração radial, na verdade, é a aceleração centrípeta.
Para o carrinho no topo, onde a velocidade é :
Para o carrinho na base, onde a velocidade é :
Passo 3
Alguem aí ouviu falar em atrito no enunciado da questão? Bom, se ninguém ouviu é porque não existe, e se não existe no nosso sistema há conservação de energia mecânica :
Agora o que temos que fazer é inserir as energias potencial gravitacional e cinética , no contexto da nossa questão. Vamos lá!
No ponto b, base do loop, o carrinho está na origem do referencial, mas com uma determinada velocidade . Logo só há energia cinética nesse ponto, que chamaremos de . Já quando o carrinho, executa o looping em , encontra-se a uma altura em relação ao solo com uma dada velocidade . Consequentemente, energia potencial gravitacional e cinética estão presentes nesse momento, denominadas e . Igualemos então as energias final e inicial:
Mas, no chegamos que
Falta agora dar o golpe final: substituir na fórmula de , obtida anteriormente:
Resposta
A pessoa sentirá vezes o próprio peso, pois a normal.