Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 5.Exercícios e Problemas - Ex. 14
5.14E Suponha que entre o bloco e a superfície da rampa da Figura 5.14 haja um coeficiente de atrito cinético . Sendo a velocidade inicial do bloco, calcule: A) o tempo gasto no deslizamento; B) a velocidade final do bloco.
Passo 1
Belejóia galerinha bonita, na letra (A) o enunciado pediu pra gente encontrar o tempo que nosso bloco da levará pra chegar a base da rampa.
Mas calma lá meu patrão, porque quando o enunciado diz que o coeficiente de atrito estático é tal que , ele tá nos dando o bizu de que a força de atrito não é suficiente para frear o movimento e dessa forma o bloco vai deslizar com uma aceleração constante. E se essa aceleração é constante quer dizer que as equações do Movimento Uniformemente Acelerado (MUV) se aplicam a esse movimento MUAHAHAHAH
E pelas equações do MUV, temos que a aceleração é dada pela fórmula:
Logo o tempo será:
Passo 2
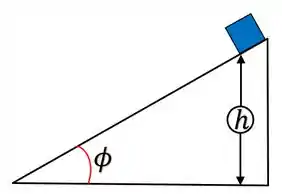
Iradoso, agora que a coisa já começou a ficar sagaz podemos encontrar primeiro nosssa aceleração, saca só, a figura 5.14 é dada pra gente como:
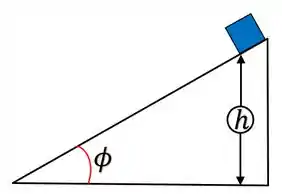
Sabendo disso podemos traçar um diagrama de forças pro nosso bloco:
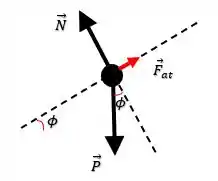
Onde é a força peso do bloco, enquanto e são as forças normal e de atrito respectivamente. Belezoca, além disso, no eixo da rampa a componente da força peso será:
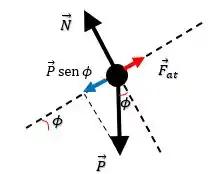
Dessa forma a força resultante no eixo da rampa vai ser o somatório da componente da força peso com a força de atrito:
E como a força peso é e a força de atrito é temos que:
Onde é a massa do bloco e é a gravidade. Maaasss a força normal também é uma componente da força peso, dada por:
Logo a força resultante será:
E como toda força existente, podemos expressar a força resultante de acordo com a fórmula , onde é a massa do bloco e será nossa aceleração resultante:
Assim, teremos que a força resultante será:
Cortando a massa dos dois lados e colocando a gravidade em evidência, descobrimos que a aceleração resultante será:
Descobrirmos então que a aceleração do nosso bloco quando está sujeito à uma força de atrito é dada por essa relação fofinha ai!
Passo 3
Já para a velocidade, como estamos falando de um MUV, podemos também aplicar a equação de Torricelli, que diz que:
Onde é a distância total percorrida na rampa, dada por:
Logo a equação de Torricelli fica assim:
Sendo assim a variação da velocidade será:
Portanto:
Passo 4
Sendo assim, o tempo total gasto para se chegar até a base da rampa é:
E passando o denominador pra dentro da raiz, obtemos:
E por fim manipulando nossa expressão chegamos em:
E de quebra a gente também já descobrirmos nossa letra (B) que pedia pra encontrar a velocidade final . Portanto o tempo e a velocidade são:
