Na Fig. 6-62, um bloco de se move para cima ao longo de um plano inclinado de ângulo ao mesmo tempo em que sofre a ação de uma força horizontal de módulo . O coeficiente de atrito cinético entre o bloco e o plano é . Quais são (a) o módulo e (b) o sentido (para cima ou para baixo ao longo do plano inclinado) da aceleração do bloco? A velocidade inicial do bloco é . (c) Que distância o bloco sobe no plano? (d) Depois de atingir o ponto mais alto, o bloco permanece em repouso ou escorrega para baixo?
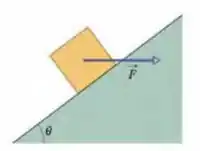
Passo 1
Vamos iniciar esta questão fazendo o DCL para o bloco:
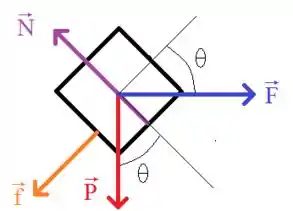
A partir da ilustração podemos visualizar melhor a disposição das forças e aplicar a segunda lei de Newton aos eixos:
Aqui supomos que a aceleração está no sentido positivo do eixo , ou seja, aponta para cima. Caso essa suposição seja falsa, encontraremos o valor da aceleração negativa ao resolver este problema.
Além disso, devemos nos lembrar que a força de atrito cinético pode ser calculado usando a seguinte relação:
Passo 2
Vamos iniciar, isolando a aceleração na e já substituindo a :
Como não temos o módulo da normal, podemos obtê-lo usando a :
Substituindo esta expressão na equação da aceleração:
Substituindo os valores dado no problema:
Como encontramos a aceleração negativa, isto mostra que supomos o sentido errado inicialmente e, portanto, a aceleração aponta para baixo.
Passo 3
Para determinar a distância que o bloco sobe no plano inclinado, podemos usar a equação de Torricelli, uma vez que temos a velocidade inicial, a velocidade final e sabemos que este é um movimento com aceleração constante, calculada no passo anterior. Assim:
Isolando :
Passo 4
Para determinar se o bloco permanecerá em repouso quando alcançar a altura máxima, vamos aplicar a segunda lei de Newton, no qual o eixo está em equilíbrio:
Isolando :
Substituindo os valores:
Com este valor em mãos, vamos compará-lo com o módulo da força de atrito cinético, pois somente temos o coeficiente de atrito cinético em mãos. Para tanto, devemos lembrar que a força de atrito estático deve ser sempre maior ou igual a força de atrito cinético, nunca maior. Assim, se o valor da força de atrito cinético for maior do que os calculado acima, então o bloco permanecerá em repouso. Para calcualr a força de atrito cinético, vamos substituir a na :
Como , então o bloco permanecerá em repouso ao atingir a altura máxima.
Resposta
- ;
- ;
- ;
- .