Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 105
Um operário aplica uma força constante de módulo a uma caixa de que está inicialmente em repouso no piso horizontal de um armazém. Após a caixa ter percorrido uma distância de , sua velocidade é . Qual é o coeficiente de atrito cinético entre a caixa e o piso?
Passo 1
Oláaaa, querido! Temos uma caixa se movendo na horizontal por causa de uma força de . E aí ele quer saber o coeficiente de atrito da caixa com o piso.
Temos esse diagrama de corpo livre:
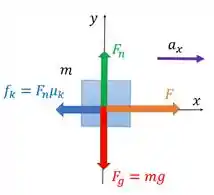
Para resolver essa a gente precisa usar a segunda lei de Newton, mas não temos a aceleração do bloco .
Mas fica tranquiiiiilo, porque podemos perceber que este é um movimento com aceleração constante (já que é constante) e o enunciado nos deu alguns dados para a gente achar essa .
Ele deu a velocidade inicial (o bloco sai do repouso), velocidade final e o deslocamento, então podemos calcular a aceleração usando a equação de Torricelli:
Assim, isolando e substituindo os valores:
Agora a gente vai aplicar a segunda lei de Newton para esse movimento e achar . Bora
Passo 2
De acordo com a 2° Lei de Newton no eixo x para o bloco, vamos ter
Aí nessa direção, a gente temos , no sentido negativo se opondo ao movimento. E temos também a força que aponta para positivo.
O somatório de forças fica
Agora a segunda lei de Newton para esse mesmo bloco para a direção , sabendo que :
Nessa direção temos a força normal para a parte positiva e a força peso para baixo. O somatório fica:
Passo 3
Substitindo em :
Isolando :
Substituindo os valores